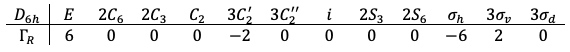Advanced Chemistry - Mono Mole

July 26, 2024November 13, 2024

The Hückel method

The Hückel method is a semi-empirical method that makes additional assumptions to the $\pi$ -electron approximation in order to determine the energies of $\pi$ molecular orbitals in planar molecules that are conjugated.

Question

What is a semi-empirical method?

Answer

A semi-empirical method combines theoretical approximations with experimental data to derive useful parameters, such as the energy of a molecular orbital (MO).

Like the $\pi$ -electron approximation, the Hückel method assumes that $\sigma$ valence electrons in planar conjugated organic compounds are relatively unreactive for reactions that do not involve in breaking these $\sigma$ bonds. Furthermore, they are assumed not to interact with the $\pi$ valence electrons, which participate in many reactions. Consequently, the $\sigma$ valence electrons are ignored in deriving the energies of the MOs.

To solve for the energies $E_{\pi}$ of $\pi$ -electron MOs, we refer to eq157 of the Hartree-Fock-Roothaan method. The total wavefunction is $\psi_{\pi}=\hat{A}\Pi_{i=1}^{n_{\pi}}\phi_i$ , where $\hat{A}$ is the antisymmetriser and $\phi_i=\sum_{r=1}^{n_c}c_{ir}\chi_r$ . The index $n_c$ refers to the number of carbon atoms forming the conjugated framework of the planar molecule, while $\phi_r$ is a real and normalised $2p_z$ orbital of the $r$ -th carbon atom. Non-trivial solutions are given by the secular determinant:

$\vert H_{rs}-E_iS_{rs}\vert=0$

where

$H_{rs}=\langle \phi_r\vert H_{eff}\vert\phi_s\rangle$ is known as the Coulomb integral if $r=s$ .

$H_{rs}=\langle \phi_r\vert H_{eff}\vert\phi_s\rangle$ is known as the resonance integral if $r\neq s$ .

$S_{rs}=\langle \phi_r\vert \phi_s\rangle$ is the normalisation expression of $\phi_r$ if $r=s$ .

$S_{rs}=\langle \phi_r\vert \phi_s\rangle$ is known as the overlap integral if $r\neq s$ .

$E_i$ is the eigenvalue associated with $\psi_i$ .

Unlike ab initio methods, the exact form of the effective Hamiltonian $H_{eff}$ in $H_{rs}$ is not important (see below for explanation). The additional assumptions used in the Hückel method are:

$H_{rs}=\biggr\{\begin{matrix}\alpha,& r=s\\\beta,&r\neq s\;for\;adjacent\;carbon\;atoms\\0,&otherwise\end{matrix}$

$S_{rs}=\delta_{rs}$

In other words, all Coulomb integrals (interaction energy) have the same value of $\alpha$ , which is reasonable if all the atoms forming the conjugated framework are the same. It follows that $H_{rs}=\beta$ for adjacent atoms is similarly a good approximation. From ab initio calculations, both $\alpha$ and $\beta$ are negative. As non-adjacent carbons atoms are well separated in space, the conjecture that $H_{rs}=0$ for non-adjacent carbons atoms $r$ and $s$ is also reasonable. The integral $S_{rr}=1$ is a result of the normalisation of $2p_z$ orbitals. However, $S_{rs}=0$ for adjacent carbon atoms is a poor approximation because $2p_z$ orbitals of adjacent carbon atoms are not orthogonal to one another. In reality, the overlap of $2p_z$ orbitals of adjacent carbon atoms leads to a stabilisation (lower energy) of bonding MOs and a destabilisation (increase in energy) of antibonding MOs. Nevertheless, the relative order of the MOs along the energy axis generally remains unchanged.

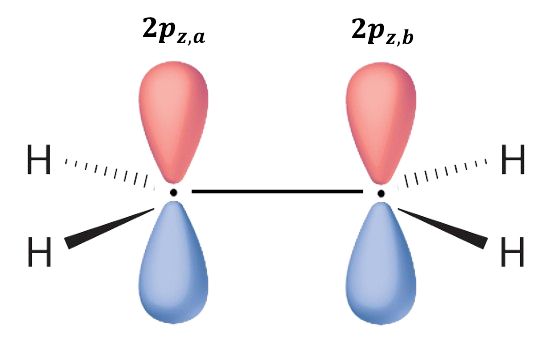
Let’s look at a simple example: ethene. The wavefunction is $\psi_{\pi}=c_12p_{z,a}+c_22p_{z,b}$ and the secular determinant is

$\begin{vmatrix}H_{11}-E_iS_{11}&H_{12}-E_iS_{12}\\H_{21}-E_iS_{21}&H_{22}-E_iS_{22}\end{vmatrix}=0$

Since the $2p_z$ orbitals are real and $H_{eff}$ is Hermitian, $S_{rs}=S_{sr}$ and $H_{rs}=H_{sr}$ . Furthermore, $S_{rr}=1$ and we have

$\begin{vmatrix}\alpha-E_i&\beta\\\beta&\alpha-E_i\end{vmatrix}=0$

This implies that $E_i=\alpha\pm\beta$ and the ground state electron configuration of the $\pi$ electrons in ethene is

Consequently, the Hückel method provides a quick way of predicting the number and order of a conjugated molecule’s valence MOs that likely to participate in a reaction, without explicitly specifying the Hamiltonian. The parameters $\alpha$ and $\beta$ are adjusted to give the best fit to experimental data, which is why the Hückel method is considered a semi-empirical method. The total ground state $\pi$ electronic energy of ethene is $E_{\pi}=2\alpha+2\beta$ .

Question

Show that i) $c_1=c_2$ when $E_1=\alpha+\beta$ and $c_2=-c_1$ when $E_2=\alpha-\beta$ , and that ii) the normalisation constant $N$ of $\psi_{\pi}=c_1(\phi_1+\phi_2)$ is $N=\frac{1}{\sqrt{2}}$ .

Answer

i) Multiplying the eigenvalue equation $H_{eff}(c_1\phi_1+c_2\phi_2)=E_i(c_1\phi_1+c_2\phi_2)$ by $c_1\phi_1+c_2\phi_2$ , integrating over all space and using the Hückel assumptions, we get

$(c_1^2+c_2^2)(\alpha-E_i)+2c_1c_2\beta=0$

For $E_1=\alpha+\beta$ and $E_2=\alpha-\beta$ , we have $c_1=c_2$ and $c_2=-c_1$ , respectively.

Therefore, the occupied MO wavefunction and unoccupied MO are $\psi_{\pi}=c_1(\phi_1+\phi_2)$ and $\psi_{\pi}=c_1(\phi_1-\phi_2)$ respectively. Since the two electrons occupying $\psi_{\pi}=c_1(\phi_1+\phi_2)$ lead to a stable molecule, the MO is known as the bonding MO. The higher energy MO, which obviously results in a relatively less state when occupied, is known as the antibonding MO.

ii)
$\int N(\phi_1+\phi_2)^*N(\phi_1+\phi_2)d\tau=1$

$N^2\biggr$\int \phi_1^*\phi_1d\tau+\phi_1^*\phi_2d\tau+\cdots\biggr$=1$

Since $S_{rs}=\delta_{rs}$ , we have $N=\frac{1}{\sqrt{2}}$

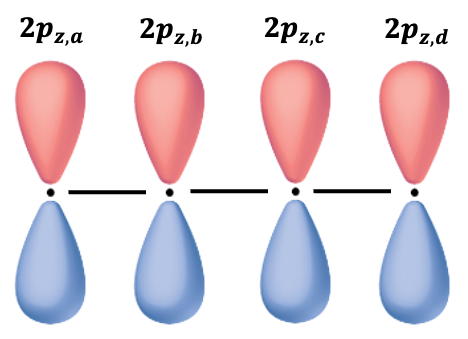
Let’s consider another molecule: 1,3-Butadiene. The secular determinant is:

$\begin{vmatrix}H_{11}-E_iS_{11}&H_{12}-E_iS_{12} &H_{13}-E_iS_{13}&H_{14}-E_iS_{14}\\H_{21}-E_iS_{21}&H_{22}-E_iS_{22} &H_{23}-E_iS_{23}&H_{24}-E_iS_{24}\\H_{31}-E_iS_{31}&H_{32}-E_iS_{32} &H_{33}-E_iS_{33}&H_{34}-E_iS_{34}\\H_{41}-E_iS_{41}&H_{42}-E_iS_{42} &H_{43}-E_iS_{43}&H_{44}-E_iS_{44}\end{vmatrix}=0$

The Hückel assumptions give

$\begin{vmatrix}\alpha-E_i&\beta &0&0\\\beta&\alpha-E_i &\beta&0\\0&\beta &\alpha-E_i&\beta\\0&0 &\beta&\alpha-E_i\end{vmatrix}=0$

Using the determinant identity $\vert cA\vert=c^n\vert A\vert$ , we multiply both sides of the above equation by $\frac{1}{\beta^4}$ to yield

$\begin{vmatrix}x&1&0&0\\1&x &1&0\\0&1 &x&1\\0&0 &1&x\end{vmatrix}=0$

where $x=\frac{\alpha-E_i}{\beta}$ .

Expanding the determinant, we have $x^4-3x^2+1=0$ . The roots to the polynomial are $x=\pm\sqrt{\frac{3+\sqrt{5}}{2}},\pm\sqrt{\frac{3-\sqrt{5}}{2}}$ and the energies of the MOs are

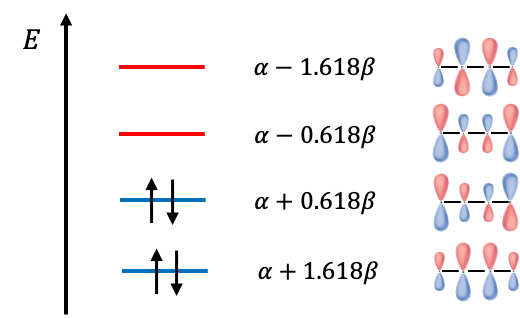
If we regard two $\pi$ electrons in 1,3-Butadiene as localised between carbons atoms $a$ and $b$ , and another two between carbon atoms $c$ and $d$ , we can compare the total ground state $\pi$ electronic energy of 1,3-Butadiene with that of two molecules of ethene. The difference of $0.472\beta$ implies an energy stabilisation for 1,3-Butadiene that is due to the delocalisation of electrons over the length of the molecule, rather than being localised.

The general form of the wavefunction for the four MOs is $\psi_{\pi}=c_1\phi_1+c_2\phi_2+c_3\phi_3+c_4\phi_4$ . To determine each individual wavefunction, we apply the Hückel assumptions to eq157, giving

$(\alpha-E_i)c_1+\beta c_2=0\;\;\;\;\;\;\;\;162$

$\beta c_1+(\alpha-E_i) c_2+\beta c_3=0\;\;\;\;\;\;\;\;163$

$\beta c_2+(\alpha-E_i) c_3+\beta c_4=0\;\;\;\;\;\;\;\;164$

$\beta c_3+(\alpha-E_i) c_4=0\;\;\;\;\;\;\;\;165$

From eq162 and eq165, we have

$c_1=-\frac{\beta}{\alpha-E_i} c_2\;\;\;\;\;\;\;\;166$

$c_4=-\frac{\beta}{\alpha-E_i} c_3\;\;\;\;\;\;\;\;167$

Substituting eq166 in eq163 gives $[-\beta^2+(\alpha-E_i)^2]c_2+\beta(\alpha-E_i)c_3=0$ . When $E_i=E_1=\alpha+\sqrt{\frac{3+\sqrt{5}}{2}}\beta$ , we have $c_2=c_3$ .

Substituting $c_2=c_3$ in eq166 and comparing with eq167, $c_1=c_4$ . It follows that $c_1=c_4=0.618c_2=0.618c_3$ . Therefore, $\psi_1=c_2(0.618\phi_1+\phi_2+\phi_3+0.618\phi_4)$ , which becomes $\psi_1=0.3717\phi_1+0.6015\phi_2+0.6015\phi_3+0.3717\phi_4$ after normalisation. Using the same logic, we have

$\psi_2=0.6015\phi_1+0.3717\phi_2-0.3717\phi_3-0.6015\phi_4$

$\psi_3=0.6015\phi_1-0.3717\phi_2-0.3717\phi_3+0.6015\phi_4$

$\psi_4=0.3717\phi_1-0.6015\phi_2+0.6015\phi_3-0.3717\phi_4$

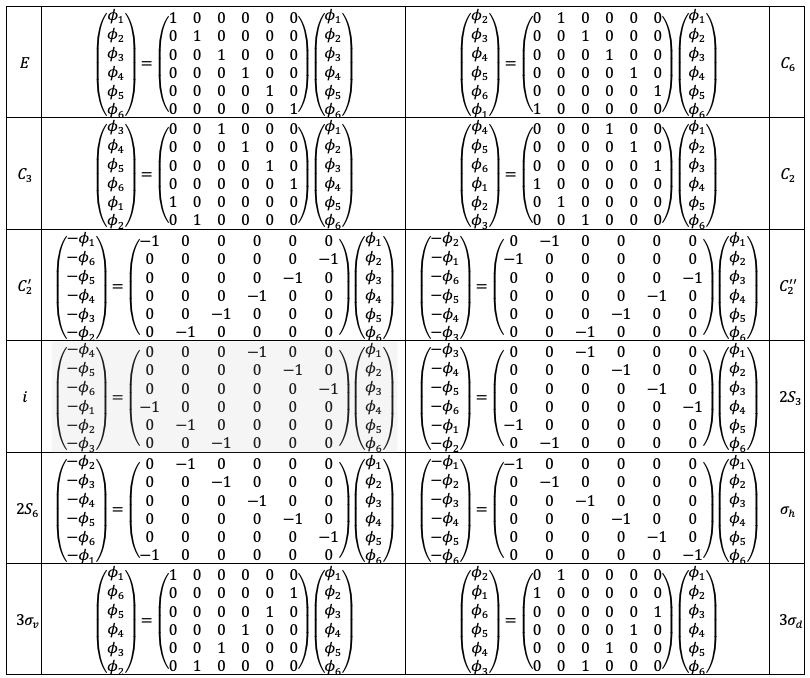
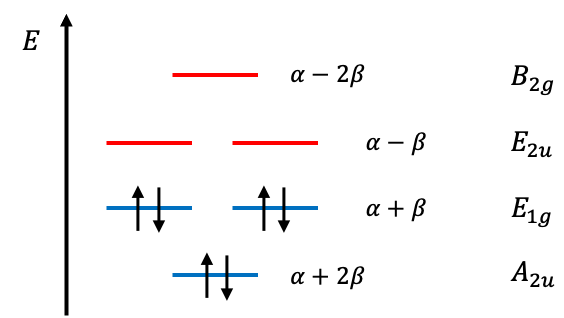
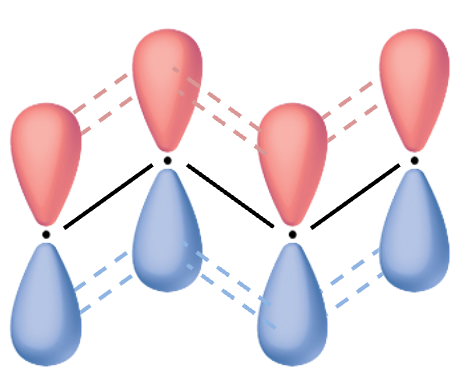
For more complicated molecules, such as benzene, the Hückel method is combined with group theory to derive the wavefunctions and solve for their associated eigenvalues.

Previous article: The $\pi$ -electron approximation

Content page of computational chemistry

Content page of advanced chemistry

Main content page

July 26, 2024September 23, 2024

Group theory and its applications in organic chemistry

Group theory plays a pivotal role in understanding molecular symmetry and electronic properties in organic chemistry, particularly when applied to the Hückel method.

Consider the benzene molecule. As the Hückel method is based on the $\pi$ -electron approximation, which treats $\pi$ electrons separately from $\sigma$ electrons, the six $2p_z$ carbon orbitals of benzene are used as a basis to generate a representation of the $D_{6h}$ point group, which the molecule belongs to.

By selecting these six $2p_z$ orbitals as a basis, their corresponding wavefunctions form a set of linearly independent wavefunctions that satisfy the effective Hamiltonian $H_{eff}$ of the $\pi$ -electron approximation of benzene. This implies that any linear combination of these six wavefunctions is associated with an eigenvalue of $H_{eff}$ . Since molecular orbitals (MOs) are formed by the combination of atomic orbitals, these linear combinations represent MOs. To generate a set of orthogonal MOs of $H_{eff}$ , we let the $D_{6h}$ symmetry operations act on the basis set to produce the following results:

The transformation matrices form a reducible representation of the point group with the following traces:

Using eq27a, $\Gamma_R$ is decomposed to $\Gamma_R=B_{2g}\oplus E_{1g}\oplus A_{2u}\oplus E_{2u}$ .

In other words, the matrices of $\Gamma_R$ can undergo a similarity transformation to yield block-diagonal matrices of the same form. Each block-diagonal matrix is composed of the direct sum of the four irreducible representations $B_{2g}$ , $E_{1g}$ , $A_{2u}$ and $E_{2u}$ . Since the number of orthogonal basis functions of an irreducible representation corresponds to the dimension of the representation, there are a total of six orthogonal basis functions for $\Gamma_R$ (one each for $B_{2g}$ and $A_{2u}$ , and two each for $E_{1g}$ and $E_{2u}$ ). These six basis functions can be generated using the projection operator.

Applying the projection operator on any $2p_z$ -orbital wavefunction, for instance $\phi_1$ , for the 1-dimensional irreducible representations of $B_{2g}$ and $A_{2u}$ , we have

$\hat{P}^{B_{2g}}\phi_1=\phi_1-\phi_2+\phi_3-\phi_4+\phi_5-\phi_6$

$\hat{P}^{A_{2u}}\phi_1=\phi_1+\phi_2+\phi_3+\phi_4+\phi_5+\phi_6$

As there are two basis functions each for the 2-dimensional irreducible representations $E_{1g}$ and $E_{2u}$ , we apply the projection operator on two $2p_z$ -orbital wavefunctions, for instance $\phi_1$ and $\phi_2$ , to give

$\hat{P}^{E_{1g}}\phi_1=\phi_1+\frac{1}{2}\phi_2-\frac{1}{2}\phi_3-\phi_4-\frac{1}{2}\phi_5+\frac{1}{2}\phi_6$

$\hat{P}^{E_{1g}}\phi_2=\frac{1}{2}\phi_1+\phi_2+\frac{1}{2}\phi_3-\frac{1}{2}\phi_4-\phi_5-\frac{1}{2}\phi_6$

$\hat{P}^{E_{2u}}\phi_1=\phi_1-\frac{1}{2}\phi_2-\frac{1}{2}\phi_3+\phi_4-\frac{1}{2}\phi_5-\frac{1}{2}\phi_6$

$\hat{P}^{E_{2u}}\phi_2=-\frac{1}{2}\phi_1+\phi_2-\frac{1}{2}\phi_3-\frac{1}{2}\phi_4+\phi_5-\frac{1}{2}\phi_6$

Some of these symmetry-adapted linear combinations (SALCs) are not orthogonal to one another. As linear combinations of basis functions that transform according to an irreducible representation of a point group also belong to the same irreducible representation, we can take linear combinations of $\hat{P}^{E_{1g}}\phi_1$ and $\hat{P}^{E_{1g}}\phi_2$ (and $\hat{P}^{E_{2u}}\phi_1$ and $\hat{P}^{E_{2u}}\phi_2$ ) to produce four SALCs that are orthogonal to $\hat{P}^{B_{2g}}\phi_1$ and $\hat{P}^{A_{2u}}\phi_1$ . The six orthogonal SALCs, after normalisation, are

Question

How do we normalise $\psi=N(2\phi_1-\phi_2-\phi_3+2\phi_4-\phi_5-\phi_6)$ , where $N$ is a constant?

Answer

$\int N\psi^*N\psi d\tau=1$

$N^2\int\biggr$4\int\psi_1^*\psi_1d\tau-2\int\psi_1^*\psi_2 d\tau+\cdots\biggr$=1$

Since $S_{rs}=\delta_{rs}$ , we have $N=\frac{1}{2\sqrt{3}}$ .

The Hückel method assumes that

$H_{rs}=\biggr\{\begin{matrix}\alpha,& r=s\\\beta,&r\neq s\;for\;adjacent\;carbon\;atoms\\0,&otherwise\end{matrix}$

$S_{rs}=\delta_{rs}$

where

$H_{rs}=\langle \phi_r\vert H_{eff}\vert\phi_s\rangle$ is known as the Coulomb integral if $r=s$ .

$H_{rs}=\langle \phi_r\vert H_{eff}\vert\phi_s\rangle$ is known as the resonance integral if $r\neq s$ .

$S_{rs}=\langle \phi_r\vert \phi_s\rangle$ is the normalisation expression of $\phi_r$ if $r=s$ .

$S_{rs}=\langle \phi_r\vert \phi_s\rangle$ is known as the overlap integral if $r\neq s$ .

To solve for the energies $E_{\pi}$ of $\pi$ -electron MOs, we refer to eq157 of the Hartree-Fock-Roothaan method. The total wavefunction is $\Psi_{\pi}=\hat{A}\Pi_{i=1}^{6}\psi_i$ , where $\hat{A}$ is the antisymmetriser and $\psi_i=\sum_{r=1}^{6}c_{ir}\phi_r$ . Non-trivial solutions are given by the secular determinant:

$\vert H'_{rs}-E_iS'_{rs}\vert=0\;\;\;\;\;\;\;\;109$

$H'_{rs}=\langle \psi_r\vert H_{eff}\vert\psi_s\rangle$ is known as the Coulomb integral if $r=s$ .

$H'_{rs}=\langle \psi_r\vert H_{eff}\vert\psi_s\rangle$ is known as the resonance integral if $r\neq s$ .

$S'_{rs}=\langle \psi_r\vert \psi_s\rangle$ is the normalisation expression of $\phi_r$ if $r=s$ .

$S'_{rs}=\langle \psi_r\vert \psi_s\rangle$ is known as the overlap integral if $r\neq s$ .

$E_i$ is the eigenvalue associated with $\psi_i$ .

Question

Show that $H'_{11}=\alpha+2\beta$ .

Answer

$H'_{11}=\frac{1}{6}\langle\phi_1+\phi_2+\phi_3+\phi_4+\phi_5+\phi_6\vert H_{eff}\vert \phi_1+\phi_2+\phi_3+\phi_4+\phi_5+\phi_6\rangle$

Expanding the integral and using the Hückel assumptions, we have $H'_{11}=\alpha+2\beta$ . Similarly,

$H'_{22}=\alpha+\beta$

$H'_{33}=\alpha+\beta$

$H'_{44}=\alpha-\beta$

$H'_{55}=\alpha-\beta$

$H'_{66}=\alpha-2\beta$

$H'_{rs}=0\;\;\;for\;\;r\neq s$

$S'_{rs}=\delta_{rs}$

Eq109 becomes

${\begin{vmatrix}\alpha+2\beta-E_1&0 &0&0 &0&0\\0&\alpha+\beta-E_2&0 &0&0&0\\0&0&\alpha+\beta-E_3 &0&0&0\\0&0 &0&\alpha-\beta-E_4&0&0\\0&0&0&0&\alpha-\beta-E_5&0\\0&0&0&0&0&\alpha-2\beta-E_6\end{vmatrix}=0}$

Using the determinant identity $\vert cA\vert=c^n\vert A\vert$ , we multiply both sides of the above equation by $\frac{1}{\beta^6}$ to give

$\begin{vmatrix}x+2&0 &0&0 &0&0\\0&x+1&0 &0&0&0\\0&0&x+1 &0&0&0\\0&0 &0&x-1&0&0\\0&0&0&0&x-1&0\\0&0&0&0&0&x-2\end{vmatrix}=0$

where $x=\frac{\alpha-E_i}{\beta}$ .

Using the determinant identity $\vert A\vert=\Pi_{i=1}^na_{ii}$ if $A$ is diagonal, we have $x=\pm 2,\pm 1,\pm 1$ . Therefore, $E_1=\alpha+2\beta$ , $E_2=\alpha+\beta$ , $E_3=\alpha+\beta$ , $E_4=\alpha-\beta$ , $E_5=\alpha-\beta$ and $E_1=\alpha-2\beta$ , giving the following MO diagram:

The total ground state $\pi$ electronic energy of benzene is $E_{\pi}=6\alpha+8\beta$ . If we regard two $\pi$ electrons in benzene as localised between carbons atoms 1 and 2, another two between 3 and 4, and another two between 5 and 6, we can compare the total ground state $\pi$ electronic energy of benzene with that of three molecules of ethene. The difference of $2\beta$ implies an energy stabilisation for benzene that is due to the delocalisation of electrons over the benzene ring, rather than being localised.

Next article: Group theory and its applications in inorganic chemistry

Previous article: Group theory and infra-red spectroscopy

Content page of group theory

Content page of advanced chemistry

Main content page

July 26, 2024September 6, 2024

The π-electron approximation

The $\pi$ -electron approximation is a method for determining the energies of planar conjugated organic compounds by treating the $\pi$ electrons separately from the $\sigma$ electrons.

In this approximation, $\sigma$ valence electrons in conjugated organic compounds are assumed to form the planar molecular framework. They are considered relatively unreactive for reactions that do not involve in breaking these $\sigma$ bonds. $\pi$ valence electrons, on the other hand, participate in many reactions. They are perceived as moving in some fixed electrostatic potential due to the $\sigma$ valence electrons.

If we further assume that the total valence wavefunction of a planar conjugated organic compound has the separable form $\psi=\psi_{\sigma}(1,2,\cdots,n_{\sigma})\psi_{\pi}(1,2,\cdots,n_{\pi})$ , we can express the Hamiltonian $H$ as

$H=H_{\sigma}+H_{\pi}$

where

$H_{\sigma}=-\frac{\hbar^{2}}{2m_e}\sum_{i=1}^{n_{\sigma}}\nabla_i^{\;2}-\sum_{i=1}^{n_{\sigma}}\frac{Ze^{2}}{4\pi\varepsilon_0r_i}+\sum_{i=1}^{n_{\sigma}-1}\sum_{j=i+1}^{n_{\sigma}}\frac{e^{2}}{4\pi\varepsilon_0r_{ij}}$

$H_{\pi}=-\frac{\hbar^{2}}{2m_e}\sum_{i=1}^{n_{\pi}}\nabla_i^{\;2}-\sum_{i=1}^{n_{\pi}}\frac{Ze^{2}}{4\pi\varepsilon_0r_i}+\sum_{i=1}^{n_{\pi}-1}\sum_{j=i+1}^{n_{\pi}}\frac{e^{2}}{4\pi\varepsilon_0r_{ij}}+\sum_{i=1}^{n_{\pi}}\sum_{j=1}^{n_{\sigma}}\frac{e^{2}}{4\pi\varepsilon_0r_{ij}}$

$\nabla_i^{\;2}=\frac{\partial^{2}}{\partial x_i^{\;2}}+\frac{\partial^{2}}{\partial y_i^{\;2}}+\frac{\partial^{2}}{\partial z_i^{\;2}}$

$r_i=\sqrt{x_i^{\;2}+y_i^{\;2}+z_i^{\;2}}$

$r_{ij}=\vert\boldsymbol{\mathit{r}}_i-\boldsymbol{\mathit{r}}_j\vert=\sqrt{(x_i-x_j)^{2}+(y_i-y_j)^{2}+(z_i-z_j)^{2}}$

It follows that the total energy $E$ of the valence electrons is

$E=E_{\sigma}+E_{\pi}$

where $E_{\sigma}=\int\psi_{\sigma}^*H_{\sigma}\psi_{\sigma}d\tau_{\sigma}$ and $E_{\pi}=\int\psi_{\pi}^*H_{\pi}\psi_{\pi}d\tau_{\pi}$ .

As we have assumed that $\pi$ valence electrons are involved in reactions, we need only to solve for $E_{\pi}$ . This is done using eq157 of the Hartree-Fock-Roothaan method, with $\psi_{\pi}=\hat{A}\Pi_{i=1}^{n_{\pi}}\phi_i$ , where $\hat{A}$ is the antisymmetriser and $\phi_i=\sum_{r=1}^{n_c}c_{ir}\chi_r$ . The basis functions $\chi_r$ are the $2p_z$ orbitals of the $n_c$ carbon atoms of the planar molecule.

Evaluating $E_{\pi}$ for larger molecules using the aforementioned ab initio procedure may be challenging. To streamline the computation, we can introduce additional assumptions, which leads us to the Hückel method.

Question

What does ab initio mean?

Answer

Ab initio means “from the beginning” in Latin. An ab initio method involves deriving some parameters from first principles and not from experimental data. The Hartree self-consistent field method, the Hartree-Fock method and the Hartree-Fock-Roothaan method are all ab initio methods.

Next article: The Hückel method

Previous article: Solution of the Hartree-Fock-Roothaan equations for helium

Content page of computational chemistry

Content page of advanced chemistry

Main content page

May 11, 2024December 26, 2024

Rayleigh-Jeans law

The Rayleigh-Jeans law is a flawed attempt in physics to describe the spectral radiance of electromagnetic radiation as a function of wavelength from a blackbody at a given temperature.

Consider a cube of side $L$ , filled with electromagnetic radiation in thermal equilibrium at temperature $T$ . If a tiny aperture exists in one of the walls, the radiation that it emits would exhibit the properties of an ideal blackbody. The walls, regarded as perfect conductors, provide boundary conditions for the electromagnetic waves inside the cube.

In a perfect conductor, an idealised model for real metals, electric charges can move without any resistance. An electromagnetic wave propagating in the $x$ -direction, with its electric field vector parallel to the wall, causes electrons in the conductor to move in response to the field. The movement of these electrons creates an opposing electric field that cancels out the external electric field. Given that the electric field is zero at the walls, the boundary conditions can only be satisfied by standing waves. These are waves that oscillate in place and have nodes at the cube’s walls. For example, standing waves oscillating in the $x$ -direction have wavelengths of ${\lambda_x=2L/n_x}$ , where ${n_x}$ is an integer (see below diagram).

The amplitude $A$ of each of the above standing waves can be expressed as ${A=A_0sin\frac{2\pi x}{\lambda_x}}$ , or in terms of the wave vector ${\boldsymbol{\mathit{k}}_x}$ pointing in the $x$ -direction:

$A=A_0sin$\boldsymbol{\mathit{k}}_x\cdot\boldsymbol{\mathit{x}}$=A_0sink_xx$

where ${\vert\boldsymbol{\mathit{k}}_x\vert=k_x=\frac{2\pi}{\lambda_x}=\frac{\pi n_x}{L}}$ .

Similarly, the wavelengths of the oscillation modes of the electromagnetic field in the $y$ -direction and $z$ -direction are ${\lambda_y=2L/n_y}$ and ${\lambda_z=2L/n_z}$ , respectively. Correspondingly, the magnitudes of the wave vectors are given by ${k_y=\pi n_y/L}$ and ${k_z=\pi n_z/L}$ , respectively. It follows that the wave vector $\boldsymbol{\mathit{k}}$ of the oscillation modes of the electromagnetic field in an arbitrary direction in the cube lies in a $k$ -space, which contain a cubical array of points that are $\pi/L$ apart (see Figure I below).

Since the magnitude of the wave vector $\boldsymbol{\mathit{k}}$ is ${\vert\boldsymbol{\mathit{k}}\vert=k=\sqrt{k_x^2+k_y^2+k_z^2}=\frac{\pi}{L}\sqrt{n_x^2+n_y^2+n_z^2}}$ , boundary conditions are satisfied by each ordered triple ${(k_x,k_y,k_z)}$ . In other words, every mode of oscillation of an arbitrary wave oscillating in the cube is defined by a point in the $k$ -space. We can also plot the array of modes in an $n$ -space, where the points are now unit length apart from one another (see Figure II above). Substituting ${k=2\pi/\lambda=2\pi\nu/c}$ in ${k=\frac{\pi}{L}\sqrt{n_x^2+n_y^2+n_z^2}}$ , we have

$\frac{2L}{c}\nu=\sqrt{n_x^2+n_y^2+n_z^2}=R\;\;\;\;\;\;\;\;1$

where $R$ is the radius of an octant (one-eighth of the volume of a sphere) in the $n$ -space.

For a certain value of $\nu$ , ordered triples of ${(n_x,n_y,n_z)}$ that satisfy eq1 lie on the surface of the octant. Consider the volume of the shell of the octant ${dV=\frac{1}{8}4\pi R^2dR}$ enclosed by the surfaces at $R$ and $R+dR$ . Substituting eq1 and ${\frac{2L}{c}d\nu=dR}$ in $d\nu$ , we have

$dV=4\pi\biggr$\frac{L}{c}\biggr$^3\nu^2d\nu$

Since the density $D$ of the number of modes in the $n$ -space is one per unit volume, the number of modes $Nd\nu$ within the shell is the product of $D$ and $dV$ :

$Nd\nu=4\pi\biggr$\frac{L}{c}\biggr$^3\nu^2d\nu$

As there are two independent polarisations for each mode of an electromagnetic wave (see above diagram),

$Nd\nu=8\pi\biggr$\frac{L}{c}\biggr$^3\nu^2d\nu$

Lord Rayleigh used the equipartition theorem to assume that each mode has an average energy of $\overline{E}=kT$ . Multiplying the above equation by the average energy $\overline{E}$ per mode, we have

$u(\nu)d\nu=8\pi\frac{\nu^2}{c^3}\overline{E}d\nu=\frac{8\pi\nu^2kT}{c^3}d\nu\;\;\;\;\;\;\;\;2$

where ${u(\nu)d\nu=\frac{N\overline{E}}{L^3}d\nu}$ is the energy density (average energy per mode between $\nu$ and $\nu+d\nu$ per unit volume of the cube).

Eq2 is known as the Rayleigh-Jeans law, which fails to describe the spectrum of blackbody radiation at high frequencies because it implies that radiated energy would increase without limit as $\nu$ increases, leading to what is called an ultraviolet catastrophe (see diagram below).

Next article: Planck radiation law

Previous article: Reduction of the two-particle problem to one-particle problems

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

May 11, 2024August 16, 2025

Planck radiation law

The Planck radiation law explains how a blackbody emits electromagnetic radiation at a specific temperature, based on the assumption that the energy of each oscillator in the body can only have discrete values.

In June 1900, Lord Rayleigh published the Rayleigh-Jeans law, which is now known as a flawed attempt in physics to describe the spectral radiance of electromagnetic radiation as a function of wavelength from a blackbody at a given temperature. The mistake that he made was to use the equipartition theorem to assume that each oscillation mode within a blackbody has an average energy of $\overline{E}=kT$ . In December of the same year, the German physicist Max Planck presented the Planck radiation law, which assumed that the energy of an oscillator of frequency $\nu$ came in discrete bundles:

$E_{n,\nu}=nh\nu$

where $n=0,1,2,\cdots$ and $h$ is a proportionality constant called the Planck constant.

According to the Boltzmann distribution, the probability of a mode $P_{n,\nu}$ with frequency $\nu$ associated with the state $E_{n,\nu}$ is

$P_{n,\nu}=\frac{e^{-\frac{E_{n,\nu}}{kT}}}{\sum_{n=0}^{\infty}e^{-\frac{E_{n,\nu}}{kT}}}$

The average energy $\overline{E}$ of the mode of frequency $\nu$ is

$\overline{E}=\sum_{n=0}^{\infty}E_{n,\nu}p_{n,\nu}=\frac{\sum_{n=0}^{\infty}E_{n,\nu}e^{-\frac{E_{n,\nu}}{kT}}}{\sum_{n=0}^{\infty}e^{-\frac{E_{n,\nu}}{kT}}}=h\nu\frac{\sum_{n=0}^{\infty}ne^{-\frac{nh\nu}{kT}}}{\sum_{n=0}^{\infty}e^{-\frac{n\nu}{kT}}}$

Let ${x=e^{-\frac{h\nu}{kT}}}$ .

$\overline{E}=h\nu\frac{\sum_{n=0}^{\infty}nx^n}{\sum_{n=0}^{\infty}x^n}=h\nu\biggr$\frac{x+2x^2+3x^3+\cdots}{1+x+x^2+\cdots}\biggr$=h\nu x\biggr$\frac{1+2x+3x^2+\cdots}{1+x+x^2+\cdots}\biggr$$

Substituting the Taylor series of ${\frac{1}{1-x}=1+x+x^2+\cdots}$ and ${\frac{1}{(1-x)^2}=1+2x+3x^2+\cdots}$ into the above equation gives

$\overline{E}=\frac{h\nu x}{1-x}=\frac{h\nu}{x^{-1}-1}=\frac{h\nu}{e^{\frac{h\nu}{kT}}-1}\;\;\;\;\;\;\;\;4$

Substituting eq4 into eq2 yields

$u(\nu)d\nu=\frac{8\pi h\nu^3}{c^3}\frac{1}{e^{\frac{h\nu}{kT}}-1}d\nu\;\;\;\;\;\;\;\;5$

which is the mathematical expression of the Planck distribution law.

Question

Show that in the classical limit, the average energy of a mode in eq4 is consistent with the equipartition theorem.

Answer

In the classical limit, ${h\nu\rightarrow 0}$ and we can expand ${e^\frac{h\nu}{kT}}$ as the Taylor series ${e^\frac{h\nu}{kT}=1+\frac{h\nu}{kT}+\frac{1}{2!}\biggr$\frac{h\nu}{kT}\biggr$^2+\cdots}$ . Substituting the series into eq4 and ignoring the higher powers of the series because ${\frac{h\nu}{kT}\rightarrow 0}$ , we have $\overline{E}=kT$ .

Previous article: Rayleigh-Jeans law

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

May 9, 2024June 27, 2025

Maxwell-Boltzmann distribution

The Maxwell-Boltzmann distribution $f(v)$ describes the range of speeds $v$ among gaseous molecules of an ideal gas at a given temperature $T$ .

The energy of an ideal gas molecule of mass $m$ is characterised solely by its kinetic energy $E$ . For a molecule with velocity $\hat{v}$ , its energy is ${E=\frac{1}{2}mv_x^2+\frac{1}{2}mv_y^2+\frac{1}{2}mv_z^2}$ , where ${v_x}$ , ${v_y}$ and ${v_z}$ are the velocity vector components of $\hat{v}$ in Cartesian coordinates. Given that a molecule with the velocity magnitude ${\vert\hat{v}_i\vert=v_i}$ has the same energy regardless of direction, any molecule with the ordered triple ${(v_x,v_y,v_z)}$ that lies on the surface of a sphere of radius ${v_i}$ in velocity space belongs to the energy state ${\varepsilon_i=\frac{1}{2}mv_{x,i}^2+\frac{1}{2}mv_{y,i}^2+\frac{1}{2}mv_{,i}z^2}$ (see diagram below).

The fraction of molecules in the energy state ${\varepsilon_i}$ is given by the Boltzmann distribution:

$\frac{n_i}{N}=\frac{e^{-\frac{\varepsilon_i}{kT}}}{\sum_ie^{-\frac{\varepsilon_i}{kT}}}\;\;\;\;\;\;\;\;1$

where

$k$ is the Boltzmann constant.
$T$ is the equilibrium temperature of the system.
${n_i}$ is the number of molecules in the energy state.
$N$ is the total number of molecules in the system.

In probability theory, ${\frac{n_i}{N}}$ is the probability ${p_i}$ of molecules in state $i$ , with ${\sum_ie^{-\frac{\varepsilon_i}{kT}}}$ being the normalisation constant. In other words, ${p_i\propto e^{-\frac{\varepsilon_i}{kT}}}$ , which we can rewrite as:

$f(v_x,v_y,v_z)=Ke^{-\frac{m(v_x^2+v_y^2+v_z^2)}{2kT}}\;\;\;\;\;\;\;\;2$

where ${f(v_x,v_y,v_z)}$ is the probability density function (probability per unit interval of $v$ ) of molecules in a particular energy state ${\frac{1}{2}mv_x^2+\frac{1}{2}mv_y^2+\frac{1}{2}mv_z^2}$ (we have dropped the index $i$ for convenience) and $K$ is the proportionality constant.

Since ${f(v_x,v_y,v_z)=\biggr$K'e^{-\frac{mv_x^2}{2kT}}\biggr$\biggr$K'e^{-\frac{mv_y^2}{2kT}}\biggr$\biggr$K'e^{-\frac{mv_z^2}{2kT}}\biggr$=f(v_x)f(v_y)f(v_z)}$ , where ${K'=K^{1/3}}$ ,

$f(v_x,v_y,v_z)=Ke^{-\frac{mv_x^2}{2kT}}e^{-\frac{mv_y^2}{2kT}}e^{-\frac{mv_z^2}{2kT}}\;\;\;\;\;\;\;\;3$

As the probability density function ${f(v_x,v_y,v_z)}$ is separable, its normalisation is equivalent to the separate normalisation of each of the individual functions:

$\int_{-\infty}^{\infty}f(v_x)dv_x=1\;\;\;\;\int_{-\infty}^{\infty}f(v_y)dv_y=1\;\;\;\;\int_{-\infty}^{\infty}f(v_z)dv_z=1\;\;\;\;\;\;\;\;4$

Let’s evaluate just one of the integrals in eq4 by substituting ${f(v_x)=K^{1/3}e^{-\frac{mv_x^2}{2kT}}}$ in ${\int_{-\infty}^{\infty}f(v_x)dv_x=1}$ to give

$K^{\frac{1}{3}}\int_{-\infty}^{\infty}e^{-\frac{mv_x^2}{2kT}}dv_x=1\;\;\;\;\;\;\;\;5$

Question

Show that ${\int_{-\infty}^{\infty}e^{-aX^2}dX=\sqrt{\frac{\pi}{a}}}$ .

Answer

Let ${I=\int_{-\infty}^{\infty}e^{-aX^2}dX}$ and at the same time let ${I=\int_{-\infty}^{\infty}e^{-aY^2}dY}$ since $X$ and $Y$ are dummy variables.

$I^2=\int\int_{-\infty}^{\infty}e^{-a(X^2+Y^2)}dXdY$

In polar coordinates, $r^2=X^2+Y^2,X=rcos\theta,Y=rsin\theta$ . For infinitesimal changes, the change in area $dA$ can be approximated as a rectangle with sides $r$ and $rd\theta$ (see diagram below), with $dXdY=dA=rd\theta dr$ .

So,

$I^2=\int_{0}^{2\pi}d\theta\int_{0}^{\infty}re^{-r^2}dr=2\pi\int_{0}^{\infty}re^{-r^2}dr$

Let $u=r^2\;\Rightarrow\;du=2rdr$

$I^2=2\pi\int_{0}^{\infty}re^{-au}\frac{du}{2r}=\pi\int_{0}^{\infty}e^{-au}du=\frac{\pi}{a}\;\;\Rightarrow\;\;I=\sqrt{\frac{\pi}{a}}$

Hence, eq5 becomes,

$K=\biggr$\frac{m}{2\pi kT}\biggr$^{\frac{3}{2}}\;\;\;\;\;\;\;\;6$

Substituting eq6 in eq3,

$f(v_x,v_y,v_z)=\biggr$\frac{m}{2\pi kT}\biggr$^{\frac{3}{2}}e^{-\frac{mv_x^2}{2kT}}e^{-\frac{mv_y^2}{2kT}}e^{-\frac{mv_z^2}{2kT}}\;\;\;\;\;\;\;\;7$

Eq7 is known as the Maxwell-Boltzmann distribution for the velocity vector of a molecule. The fraction of molecules ${dn_{v_xv_yv_z}/N}$ with velocity vectors in the infinitesimal range of ${v_x}$ to ${v_x+dv_x}$ , ${v_y}$ to ${v_y+dv_y}$ and ${v_z}$ to ${v_z+dv_z}$ is

$\frac{dn_{v_xv_yv_z}}{N}=f(v_x,v_y,v_z)dv_xdv_ydv_z=\biggr$\frac{m}{2\pi kT}\biggr$^{\frac{3}{2}}e^{-\frac{m(v_x^2+v_y^2+v_z^2)}{2kT}}dv_xdv_ydv_z\;\;\;\;\;\;\;\;8$

The fraction of molecules ${dn_v/N}$ with speed in the infinitesimal range of $v$ to $v+dv$ is then equivalent to the fraction of molecules with velocity vectors that lies within a spherical shell of infinitesimal thickness in velocity space (see diagram below).

In other words,

$\frac{dn_v}{N}=\biggr$\frac{m}{2\pi kT}\biggr$^{\frac{3}{2}}e^{-\frac{mv^2}{2kT}}\sum_{shell}dv_xdv_ydv_z$

where ${v^2=v_x^2+v_y^2+v_z^2}$ , and we have assumed that the volume of the shell of infinitesimal thickness is approximately equal to the sum of infinitesimal cubes, each with an infinitesimal volume of ${dv_xdv_ydv_z}$ .

Therefore, ${\sum_{shell}dv_xdv_ydv_z=4\pi v^2dv}$ and ${\frac{dn_v}{N}=f(v)dv=4\pi\biggr$\frac{m}{2\pi kT}\biggr$^{\frac{3}{2}}v^2e^{-\frac{mv^2}{2kT}}dv}$ ., which implies that the probability density function for the speed of a molecule $f(v)$ is

$f(v)=4\pi\biggr$\frac{m}{2\pi kT}\biggr$^{\frac{3}{2}}v^2e^{-\frac{mv^2}{2kT}}\;\;\;\;\;\;\;\;9$

Eq9 is known as the Maxwell-Boltzmann distribution for the speed of a molecule. It also expresses the probability of a molecule being associated with a particular energy state. For a mole of an ideal gas, we substitute $R=N_Ak$ (see this article for derivation ) in eq9 to give

$f(v)=4\pi\biggr$\frac{M}{2\pi RT}\biggr$^{\frac{3}{2}}v^2e^{-\frac{Mv^2}{2RT}}\;\;\;\;\;\;\;\;10$

where $M$ is the mass of one mole of the gas and $R$ is the gas constant.

Question

Show that the most probable speed of one mole of an ideal gas is ${v=\sqrt{\frac{2RT}{M}}}$ .

Answer

The most probable speed corresponds to the peak of the distribution (see above diagram). Carrying out the derivative ${\frac{df(v)}{dv}}$ , equating it to zero, and noting that the most probable speed $v$ is neither $0$ nor $\infty$ , we have ${v=\sqrt{\frac{2RT}{M}}}$ .

Previous article: 3rd order reaction of the type (A+B+C→P)

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

May 8, 2024August 24, 2025

Statistical entropy

Statistical entropy is a concept in thermodynamics that quantifies the number of different ways a system can be arranged while still maintaining its macroscopic properties.

The total energy of a system, $E$ , is given by eq5. Its total differential is:

$dE=\sum_i\varepsilon_idn_i+\sum_in_id\varepsilon_i$

Consider the transfer of heat to a closed system of particles. If the volume of the system is constant, then no work is done on the system and the energy level of each state is unchanged $d\varepsilon_i=0$ . However, the population of particles in each state $dn_i$ varies according to temperature. Hence,

$dE=\sum_i\varepsilon_idn_i\;\;\;\;\;\;\;\;26$

If we interpret $E$ as the internal energy of the system, $U$ , then according to the first law of thermodynamics of a constant volume system,

$dE=dU=dq\;\;\;\;\;\;\;\;27$

For a reversible transfer of heat, the second law of thermodynamics states that ${dS=\frac{dq}{T}}$ . Combining $dS$ , eq24a, eq26 and eq27,

$dS=k\beta\sum_i\varepsilon_idn_i\;\;\;\;\;\;\;\;28$

Substituting eq16 in eq28,

$dS=k\sum_i\biggr$\frac{\partial lnW}{\partial n_i}\biggr$dn_i+k\alpha\sum_idn_i$

Since the total number of particles for a closed system is constant, ${\sum_idn_i=0}$ and

$dS=k\sum_i\biggr$\frac{\partial lnW}{\partial n_i}\biggr$dn_i\;\;\;\;\;\;\;\;29$

Substituting eq4 in eq29, we have $dS=kdlnW$ or the integrated form:

$S=klnW\;\;\;\;\;\;\;\;30$

where $S$ is the statistical entropy.

Previous article: Boltzmann distribution

Content page of chemical thermodynamics

Content page of advanced chemistry

Main content page

May 8, 2024August 30, 2025

Boltzmann distribution

The Boltzmann distribution, formulated in 1868 by Ludwig Boltzmann, describes the probability distribution $p_i$ of objects (particles or oscillation modes) in a system over various energy states, $\varepsilon_i$ .

It is mathematically expressed as:

$p_i=\frac{n_i}{N}=\frac{e^{-\frac{\varepsilon_i}{kT}}}{\sum_ie^{-\frac{\varepsilon_i}{kT}}$

where

$k$ is the Boltzmann constant.
$n_i$ is the number of objects in the energy state $\varepsilon_i$ .
$N$ is the total number of objects in the system.

The derivation of the Boltzmann distribution equation involves the following steps:

1. Derivation of the total differential of $lnW$ .
2. Application of the Lagrange method of undetermined multipliers on the total differential of $lnW$ .
3. Simplification of solution using Stirling’s approximation.
4. Evaluation of $\beta$ .

Step 1

Consider a system with molecules randomly occupying different energy states, $\varepsilon_i$ . At any time, the configuration of the system can be represented by $\{n_0,n_1,\cdots\}$ with $n_0$ molecules in energy state $\varepsilon_0$ , $n_1$ molecules in energy state $\varepsilon_1$ , and so on. The total number of molecules is therefore:

$\sum_in_i=N\;\;\;\;\;\;\;\;i=0,1,\cdots\;\;\;\;\;\;\;\;1$

where $n_i$ is the number of molecules in the energy state $\varepsilon_i$ .

The number of ways, $W$ , to achieve an instantaneous configuration of $\{n_0,n_1,\cdots\}$ is given by the multinomial permutation:

$W=\frac{N!}{n_0!n_1!\cdots}\;\;\;\;\;\;\;\;2$

or in the natural logarithmic form:

$lnW=ln\frac{N!}{n_0!n_1!\cdots}\;\;\;\;\;\;\;\;3$

Question

Eq2 implies that the molecules are distinguishable when they are being assigned to different energy states, and that once these assignments are made, the order of molecules within each state does not matter. Why?

Answer

Boltzmann statistics is rooted in classical physics, where particles of the same type are considered distinguishable because they can be differentiated by their physical states, such as position and velocity. In contrast, particles of the same type in quantum mechanics are considered indistinguishable, which leads to different statistical distributions like Fermi-Dirac statistics for fermions and Bose-Einstein statistics for bosons.

Once the molecules are assigned to energy states, the order of the molecules within each state does not matter, because the configuration is defined only by the number of molecules in each state, not by which specific molecules occupy them.

As the number of molecules in each energy state $\{n_0,n_1,\cdots\}$ varies with time, the configuration of the system changes and so does the number of ways of achieving the new configurations. We can therefore express the LHS of eq3 in its total differential form of
${dlnW=\sum_i\biggr$\frac{\partial lnW}{\partial n_i}\biggr$_{all\;other\;n\neq n_i}dn_i}$ , or for simplicity:

$dlnW=\sum_i\biggr$\frac{\partial lnW}{\partial n_i}\biggr$dn_i\;\;\;\;\;\;\;\;4$

Let’s further define our system as a closed system with total energy, $E$ , given by:

$\sum_in_i\varepsilon_i=E\;\;\;\;\;\;\;\;i=0,1,\cdots\;\;\;\;\;\;\;\;5$

Eq5 restricts the number of configurations of the system. For example, the configurations of $\{N,0,0,\cdots\}$ and $\{N-1,1,0,\cdots\}$ cannot coexist as they have different total energies. If we assume, under the conditions imposed by eq1 and eq5, that all possible configurations of the system have the same probability of occurring, the configuration with the maximum number of ways of achieving will most likely be the one the system adopts.

Step 2

The most probable configuration is found by evaluating the maximum point for the function in eq4, i.e.

$dlnW=\sum_i\biggr$\frac{\partial lnW}{\partial n_i}\biggr$dn_i=0\;\;\;\;\;\;\;\;6$

To solve eq 6, we employ the Lagrange method of undetermined multipliers. We begin by rearranging eq1 to $n_j=N-n_0-n_1-\cdots-n_{j-1}-n_{j+1}-\cdots$ , where $n_j$ is dependent on the rest of the variables, which are all independent. Eq1 can also be written in the form of a new function, :

$g=n_0+n_1+\cdots-N=0\;\;\;\;\;\;\;\;7$

Likewise, by rearranging eq5 to ${n_k=\frac{1}{\varepsilon_k}(E-n_0\varepsilon_0-n_1\varepsilon_1-\cdots-n_{k-1}\varepsilon_{k-1}-\cdots)}$
we have another dependent variable, $n_k$ and another function:

$h=n_0\varepsilon_0+n_1\varepsilon_1+\cdots-E=0\;\;\;\;\;\;\;\;8$

This results in eq6 having two dependent variables. The total differential of $g$ and $h$ are

$dg=\sum_i\biggr$\frac{\partial g}{\partial n_i}\biggr$dn_i=0\;\;\;\;\;\;\;\;9$

and

$dh=\sum_i\varepsilon_i\biggr$\frac{\partial h}{\partial n_i}\biggr$dn_i=0\;\;\;\;\;\;\;\;10$

respectively.

Since $dg=dh=0$ , we can multiply eq9 and eq10 by the factors $\alpha$ and $-\beta$ respectively and add them to eq6 to give:

$\sum_i\biggr\[\biggr$\frac{\partial lnW}{\partial n_i}\biggr$+\alpha\biggr$\frac{\partial g}{\partial n_i}\biggr$-\beta\varepsilon_i\biggr$\frac{\partial h}{\partial n_i}\biggr$\biggr\]dn_i=0\;\;\;\;\;\;\;\;11$

The factors, $\alpha$ and $\beta$ , are called Lagrange multipliers. Two of the variables, e.g. $n_j$ and $n_k$ , are dependent variables, while the rest are independent variables. If there is some value of $\alpha$ and some value of $\beta$ that render the $j$ -th and $k$ -th terms of eq11 zero, we have

$\biggr$\frac{\partial lnW}{\partial n_j}\biggr$+\alpha\biggr$\frac{\partial g}{\partial n_j}\biggr$-\beta\varepsilon_j\biggr$\frac{\partial h}{\partial n_j}\biggr$=0\;\;\;\;\;\;\;\;12$

$\biggr$\frac{\partial lnW}{\partial n_k}\biggr$+\alpha\biggr$\frac{\partial g}{\partial n_k}\biggr$-\beta\varepsilon_k\biggr$\frac{\partial h}{\partial n_k}\biggr$=0\;\;\;\;\;\;\;\;13$

Consequently, we are left with all independent variables terms. $dn_i$ in eq11 can now vary arbitrarily, which implies that all the remaining coefficients equal to zero. Substituting eq9 and eq10 in eq11,

$\sum_i\biggr$\frac{\partial lnW}{\partial n_i}\biggr$dn_i+\alpha dg-\beta dh=0\;\;\;\;\;\;\;\;14$

Noting that $N$ and $E$ are constants, eq7 and eq8 become ${dg=dn_0+dn_1+\cdots=\sum_idn_i}$ and ${dh=dn_0\varepsilon_0+dn_1\varepsilon_1+\cdots=\sum_i\varepsilon_idn_i}$ respectively. Substituting $dg$ and $dh$ in eq14,

$\sum_i\biggr\[\biggr$\frac{\partial lnW}{\partial n_i}\biggr$+\alpha-\beta\varepsilon_i\biggr\] dn_i=0\;\;\;\;\;\;\;\;15$

Since all coefficients are now equal to zero,

$\biggr$\frac{\partial lnW}{\partial n_i}\biggr$+\alpha-\beta\varepsilon_i=0\;\;\;\;\;\;\;\;16$

Step 3

To simplify eq16, we take the natural logarithm on both sides of eq3 to give ${lnW=lnN!-\sum_iln(n_i!)}$ . Since ${lnN!=ln[N(N-1)\cdots]=lnN+ln(N-1)+\cdots=\sum_{K=1}^NlnK}$ ,

$lnW=\sum_{K=1}^NlnK-\sum_iln(n!)\;\;\;\;\;\;\;\;17$

For large $N$ , we have ${\sum_{K=1}^NlnK\approx\int_1^NlnKdK}$ . Integrating by parts, ${\int_1^NlnKdK=NlnN-N}$ . Hence, ${lnN!=\sum_{K=1}^NlnK\approx NlnN-N}$ , which is known as Stirling’s approximation. Eq17 becomes ${lnW=NlnN-N-\biggr\[\sum_in_ilnn_i-\sum_in_i\biggr\]}$ . Since, ${\sum_in_i=N}$ ,

$lnW=NlnN-\sum_in_ilnn_i\;\;\;\;\;\;\;\;18$

Substituting eq18 in eq16,

$lnN\frac{\partial N}{\partial n_i}+N\frac{\partial lnN}{\partial n_i}-\sum_j\frac{\partial n_jlnn_j}{\partial n_i}+\alpha-\beta\varepsilon_i=0\;\;\;\;\;\;\;\;19$

where we have changed the summation index from $i$ to $j$ in eq19 to discriminate the summation variable from the differentiation variable.

Since $N=n_0+n_1+\cdots$ , we have ${\frac{\partial N}{\partial n_i}=1}$ . By implicit differentiation, ${\frac{\partial lnN}{\partial n_i}=\frac{1}{N}\frac{\partial N}{\partial n_i}=\frac{1}{N}}$ and ${\frac{\partial lnn_j}{\partial n_i}=\frac{1}{n_j}\frac{\partial n_j}{\partial n_i}}$ . Furthermore, ${\frac{\partial n_j}{\partial n_i}=\delta_{ij}$ . Therefore, eq19 becomes,

$n_i=Ne^{\alpha}e^{-\beta\varepsilon_i}\;\;\;\;\;\;\;\;20$

Substituting eq20 in eq1, we have ${e^{\alpha}=1/\sum_ie^{-\beta\varepsilon_i}}$ , which when substituted in eq20 gives

$\frac{n_i}{N}=\frac{e^{-\beta\varepsilon_i}}{\sum_ie^{-\beta\varepsilon_i}}\;\;\;\;\;\;\;\;21$

Step 4

An easy way to determine the value of $\beta$ is to use the equation for the distribution of molecules of an ideal gas in a cylinder:

$\frac{n}{n_0}=e^{-\frac{N_Amg\Delta h}{RT}}\;\;\;\;\;\;\;\;22$

where

$n$ is number of molecules at a height $l$ , which implies that $n$ is number of molecules in energy state $\varepsilon_l$ .
$n_0$ is the number of molecules at a height $j$ , where $j < l$ . It follows that $n_0$ is number of molecules in energy state $\varepsilon_j$ .
$m$ is the mass of a molecule.
$g$ is the acceleration due to gravity.
$\Delta h$ is the difference in height between $l$ and $j$ .
$N_A$ is the Avogadro constant
$R$ is the universal gas constant

Since $mg\Delta h$ represents the difference in energy between states $l$ and $j$ , we can rewrite eq22 as:

$\frac{n_l}{n_j}=e^{-\frac{N_A(\varepsilon_l-\varepsilon_j)}{RT}}\;\;\;\;\;\;\;\;23$

From eq21, the fractions of molecules in energy states $l$ and $j$ are ${\frac{n_l}{N}=\frac{e^{-\beta\varepsilon_l}}{\sum_ie^{-\beta\varepsilon_i}}}$ and ${\frac{n_j}{N}=\frac{e^{-\beta\varepsilon_j}}{\sum_ie^{-\beta\varepsilon_i}}}$ respectively. Dividing ${\frac{n_l}{N}}$ by ${\frac{n_j}{N}}$ ,

$\frac{n_l}{n_j}=e^{-\beta(\varepsilon_l-\varepsilon_j)}\;\;\;\;\;\;\;\;24$

Comparing eq23 and 24, $\beta=N_A/RT$ , and introducing the constant $k=R/N_A$ (the Boltzmann constant), we have

$\beta=\frac{1}{kT}\;\;\;\;\;\;\;\;24a$

Therefore, eq21 becomes

$\frac{n_i}{N}=\frac{e^{-\frac{\varepsilon_i}{kT}}}{\sum_ie^{-\frac{\varepsilon_i}{kT}}}\;\;\;\;\;\;\;\;25$

which is the Boltzmann distribution.

The Boltzmann distribution is used to derive mathematical expressions of many scientific concepts, including the statistical entropy, the Maxwell-Boltzmann distribution, and the Planck radiation law.

Question

If the Boltzmann distribution is derived based on distinguishable particles, does it mean that the ideal gas particles described in the barometric formula of eq22 are distinguishable?

Answer

No, the ideal gas particles are indistinguishable. However, whether the particles are distinguishable or not only affects the total statistical weight $\sum_ie^{-\frac{\varepsilon_i}{kT}$ (also known as the molecular partition function) in eq25. Relative probabilities, such as those expressed by the barometric formula, do not depend on the distinguishability of the particles because the partition function cancels out in the ratio.

Next article: Statistical entropy

Previous article: Permutation and combination

Content page of chemical thermodynamics

Content page of advanced chemistry

Main content page

April 30, 2024July 17, 2024

The harmonic oscillator

A harmonic oscillator comprises a particle that is subject to a restoring force proportional to the particle’s displacment $x$ from its equilibrium position.

Consider a mass $m$ connected to a rigid support by a massless and frictionless spring (see above diagram). At equilibrium, the length of the spring is $x_0$ . Let’s assume that the only force $F$ acting on the mass is a restoring force that is directly proportional to the displacement of the mass (Hooke’s law):

$F=-kx\;\;\;\;\;\;\;\;1$

where $x=x_1-x_0$ is the displacement of the mass from its equilibrium position and $k$ is constant of proportionality called the force constant.

Question

Explain why $k$ is a measure of the stiffness of the spring.

Answer

For a particular value of $F$ , the stiffer the spring, the less the mass displaces. Since $k$ is inversely proportional to $x$ , it is a measure of the stiffness of the spring.

Substituting the equation for Newton’s 2^nd law of motion $F=ma$ in eq1, we have

$m\frac{d^2x}{dt^2}+kx=0\;\;\;\;\;\;\;\;2$

The solution to the above differential equation is $x=Asin\omega t$ , where $\omega=\sqrt{\frac{k}{m}}$ . As the displacement of the mass is defined by a wave equation, the system is called a harmonic oscillator (‘harmonic’ originates from sound waves). The mass oscillates with amplitude $A$ and frequency $\frac{\omega}{2\pi}$ (see Q&A below), and the kinetic energy $E_k$ and potential energy $U$ of the system are

$E_k=\frac{1}{2}mv^2=\frac{1}{2}m\biggr$\frac{dx}{dt}\biggr$^2=\frac{1}{2}m$A\omega cos\omega t$^2$

$U=\frac{1}{2}kx^2=\frac{1}{2}k$Asin\omega t$^2\;\;\;\;\;\;\;\;3$

Question

Explain why the mass oscillates with a frequency of $\frac{\omega}{2\pi}$ and why the potential energy of the system is equal to $\frac{1}{2}kx^2$ ?

Answer

Since $x=Asin\omega t=Asin\biggr\[\omega\biggr$t+\frac{2\pi}{\omega}\biggr$\biggr\]$ , the function repeats itself after a time $\frac{2\pi}{\omega}$ . This implies that the period $T$ of the motion of the mass is $T=\frac{2\pi}{\omega}$ and that the oscillation frequency $\nu$ is $\nu=\frac{1}{T}=\frac{\omega}{2\pi}$ .

The force exerted by a person $F_p$ in lifting an object over a distance $x$ against gravity is $F_p=\frac{W}{\Delta x}$ , where $W$ is the work done by the person. $W$ must also be the amount of potential energy the object gains, i.e. $F_p=\frac{\Delta U}{\Delta x}$ . Furthermore, the force exerted by gravity $F$ is opposite to the force exerted by the person. So, $F=-\frac{\Delta U}{\Delta x}$ and for small changes, $F=-\frac{dU}{dx}$ . Since gravitational force and elastic spring force are both conservative forces (work done is path-independent), we substitute eq1 in $F=-\frac{dU}{dx}$ to give $dU=kxdx$ . Therefore, the potential energy of a harmonic oscillator is $U=k\int_0^xxdx=\frac{1}{2}kx^2$ .

The total energy $E$ of the harmonic oscillator is

$E=\frac{1}{2}m$A\omega cos\omega t$^2+\frac{1}{2}k$Asin\omega t$^2=\frac{1}{2}kA^2$

and the Hamiltonian $H$ , which is the sum of the kinetic and potential energies of the oscillator can be expressed as

$H=\frac{p^2}{2m}+\frac{1}{2}kx^2$

Before we show how the harmonic oscillator can be used to model a vibrating diatomic molecule, we shall look at the quantum-mechanical treatment of a harmonic oscillator.

Next article: The quantum harmonic oscillator

Content page of vibrational spectroscopy

Content page of advanced chemistry

Main content page

April 30, 2024October 27, 2024

Generating function and Rodrigues’ formula for the Hermite polynomials

The generating function $g(y,t)$ for Hermite polynomials is a mathematical tool that, when expanded as a power series, yields the ratio of the Hermite polynomials $H_n(y)$ and the factorial of the summation index as its coefficients.

It can also be used to derive the normalisation constant for the wavefunctions of the quantum harmonic oscillator, and is defined as

$g(y,t)=e^{-t^2+2ty}=\sum_{n=0}^{\infty}\frac{H_n(y)}{n!}t^n=H_0(y)+H_1(y)t+\frac{1}{2!}H_2(y)t^2+\cdots\;\;\;\;\;\;\;\;33$

To prove the 2^nd equality of eq33, we take the partial derivative of $g$ with respect to $y$ to give ${\frac{\partial g(y,t)}{\partial y}=\sum_{n=0}^{\infty}\frac{dH_n(y)}{dy}\frac{t^n}{n!}}$ . Substituting eq29 in this equation, we have

${\frac{\partial g(y,t)}{\partial y}=\sum_{n=0}^{\infty}2nH_{n-1}(y)\frac{t^n}{n!}=2H_0(y)t+\frac{2(2)}{2!}H_1(y)t^2+\frac{2(3)}{3!}H_2(y)t^3+\cdots=2tg(y,t)}$

The solution to the differential equation ${\frac{\partial g(y,t)}{\partial y}-2tg(y,t)=0$ is

$g(y,t)=e^{2ty}f(t)\;\;\;\;\;\;\;\;34$

When $y=0$ , eq34 becomes

$g(0,t)=f(t)=\sum_{n=0}^{\infty}\frac{H_n(0)}{n!}t^n=H_0(0)+H_1(0)t+\frac{H_2(0)}{2!}t^2+\cdots$

Using eq19,

$f(t)=H_0(0)+\frac{H_2(0)}{2!}t^2+\frac{H_4(0)}{4!}t^4+\cdots=\sum_{n=0}^{\infty}\frac{H_{2n}(0)}{(2n)!}t^{2n}$

Using eq20,

$f(t)=\sum_{n=0}^{\infty}\frac{(-1)^n(2n)!}{(2n)!n!}t^{2n}=\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}t^{2n}$

Since the Maclaurin series expansion of $e^x$ is ${\sum_{n=0}^{\infty}\frac{x^n}{n!}}$ , we have ${f(t)=\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}t^{2n}=e^{-t^2}}$ , which completes the proof.

The generating function can be used to derive the Rodrigues formula for Hermite polynomials. From 33,

$g(y,t)=e^{-t^2+2ty}=e^{y^2-(t-y)^2}=e^{y^2}e^{-(t-y)^2}$

$\frac{\partial g(y,t)}{\partial t}=e^{y^2}\frac{\partial}{\partial t}e^{-(t-y)^2}\;\;\;\;\;\;\;\;35$

Let $f=e^{-(t-y)^2$ . We have ${\frac{\partial f}{\partial t}=-(2t-2y)e^{-(t-y)^2}}$ and ${\frac{\partial f}{\partial y}=(2t-2y)e^{-(t-y)^2}}$ . Therefore,

$\frac{\partial f}{\partial t}=-\frac{\partial f}{\partial y}\;\;\;\;\;\;\;\;36$

Substitute eq36 in eq35

$\frac{\partial g(y,t)}{\partial t}=e^{y^2}\frac{\partial}{\partial t}e^{-(t-y)^2}=(-1)e^{y^2}\frac{\partial}{\partial y}e^{-(t-y)^2}$

$\frac{\partial^n g(y,t)}{\partial t^n}=e^{y^2}\frac{\partial^n}{\partial t^n}e^{-(t-y)^2}=(-1)e^{y^2}\frac{\partial}{\partial y}\frac{\partial^{n-1}}{\partial t^{n-1}}e^{-(t-y)^2}=\\(-1)^ne^{y^2}\frac{\partial^n}{\partial y^n}e^{-(t-y)^2}\;\;\;\;\;\;\;n=1,2,\cdots\;\;\;\;\;\;\;\;37$

When $t=0$

$\frac{\partial^n g(y,t)}{\partial t^n}_{t=0}=(-1)^ne^{y^2}\frac{\partial^n}{\partial y^n}e^{-y^2}\;\;\;\;\;\;\;\;38$

From eq33

$\frac{\partial g(y,t)}{\partial t}=H_1(y)+H_2(y)t+\frac{1}{2}H_3(y)t^2+\frac{1}{6}H_4(y)t^3\cdots$

$\frac{\partial^2 g(y,t)}{\partial t^2}=H_2(y)+H_3(y)t+\frac{1}{2}H_4(y)t^2+\cdots$

$\frac{\partial^n g(y,t)}{\partial t^n}=H_n(y)+H_{n+1}(y)t+\frac{1}{2}H_{n+2}(y)t^2+\cdots$

$\frac{\partial^n g(y,t)}{\partial t^n}_{t=0}=H_n(y)\;\;\;\;\;\;\;\;39$

Substitute eq39 into eq38

$H_n(y)=(-1)^ne^{y^2}\frac{d^n}{dy^n}e^{-y^2}\;\;\;\;\;\;\;\;40$

Eq40 is the Rodrigues formula for Hermite polynomials. In other words, the Rodrigues formula for Hermite polynomials is a mathematical expression that provides a method to calculate any Hermite polynomial using differentiation.

Question

Answer

Question

Answer

Previous article: The -electron approximation

Question

Answer

Question

Answer

Next article: Group theory and its applications in inorganic chemistry

Previous article: Group theory and infra-red spectroscopy

Question

Answer

Next article: The Hückel method

Previous article: Solution of the Hartree-Fock-Roothaan equations for helium

Next article: Planck radiation law

Previous article: Reduction of the two-particle problem to one-particle problems

Question

Answer

Previous article: Rayleigh-Jeans law

Question

Answer

Question

Answer

Previous article: 3rd order reaction of the type (A+B+C→P)

Previous article: Boltzmann distribution

Question

Answer

Question

Answer

Next article: Statistical entropy

Previous article: Permutation and combination

Question

Answer

Question

Answer

Next article: The quantum harmonic oscillator

Next article: Normalisation constant for the wavefunctions of the quantum harmonic oscillator

Previous article: Taylor series of single-variable and multi-variable functions

Previous article: The $\pi$ -electron approximation