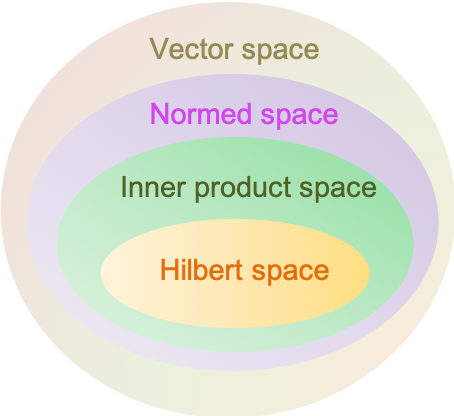
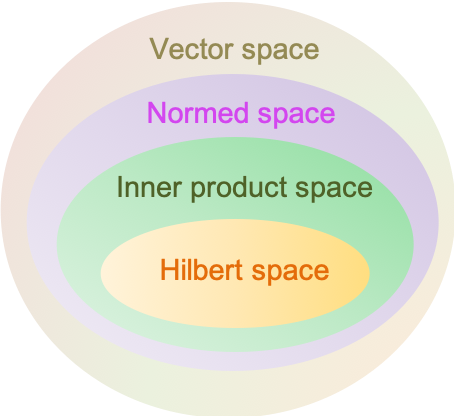
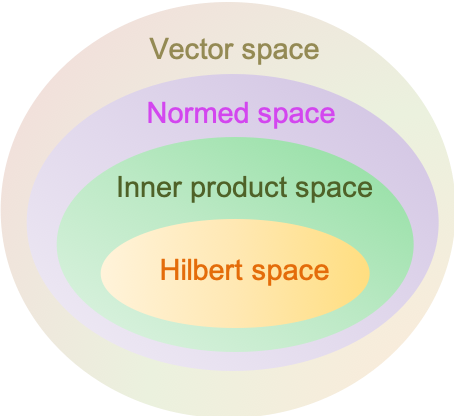
The Kronecker product, denoted by , is a multiplication method for generating a new vector space from existing vector spaces, and therefore, new vectors from existing vectors.

Consider 2 vectors spaces, e.g. and
. For
in
and
in
, we can define a new vector space,
, which consists of the vector
, where:
If the basis vectors for and
are
and
respectively, the basis for
is:

Question
Why is a new vector space?
Answer
An -dimensional vector space is spanned by
linearly independent basis vectors. The basis vectors for
and
are
and consequently, the basis vectors for are
These 6 linearly independent basis vectors therefore span a 6-dimensional space.
This implies that is
dimensional if
is
-dimensional and
is
-dimensional. Since
is a vector space, the vectors
must follow the rules of addition and multiplication of a vector space. Each vector
in the new vector space can then be written as a linear combination of the basis vectors
, i.e.
.
In general, if
then
Since the pair in
is distinct for each
vector, the Kronecker product
results in
basis vectors, which span an
vector space.
As mentioned in an earlier article, a vector space is a set of objects that follows certain rules of addition and multiplication. If the objects are matrices, we have a vector space of matrices. For example, the vector spaces of matrices and
generates a new vector space of matrices
, where
Similarly, if the objects are functions, we have a vector space of functions and the Kronecker product of two vector spaces of functions
and
generates a new vector space of functions
. If
and
are spanned by
basis functions and
basis functions respectively,
is spanned by
basis functions.
A vector space that is generated from two separate vector spaces has applications in quantum composite systems and in group theory.

Question
What is the relation between the matrix entries of A, B and C in ?
Answer
Let the matrix entries of A, B and C be ,
and
respectively, where
Using the ordering convention called dictionary order, where is determined by
and
, and
is determined by
and
, such that
and
are given by
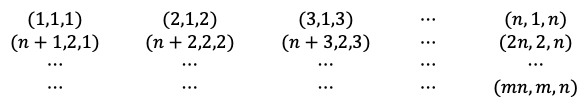
For example, if and
,

We can then express the matrix entries of as
.