Category: Intermediate Chemistry

Posted on

Virial equation of state

The virial equation of state is a mathematical expression that models the behaviour of a real gas.

Recognising van der Waals’ work, Heike Kamerlingh, another Dutch physicist, attempted to establish a more extensive equation of state and devised the virial equation of state in 1882:

pV_m=RT\left ( 1+\frac{B}{V_m}+\frac{C}{V_m^{\: 2}}+... \right )\; \; \; \; \; \; \; \; 16

The word virial is latin meaning force or energy. The RHS of eq16 suggests that the virial equation is derived using a power series.

In fact, the equation can be perceived as a Maclaurin series of van der Waals’ equation. To illustrate this, let’s multiply the right side of eq10 from the previous section by \frac{x}{x} where x=\frac{1}{V_m} to give:

p=\frac{RTx}{1-bx}-ax^2\; \; \; \; \; \; \; \; 17

A Maclaurin series for the polynomial p(x)=c_0+c_1x+c_2x^2+c_3x^3+... is in the form:

p(x)=p(0)+\frac{p'(0)}{1!}x+\frac{p''(0)}{2!}x+\frac{p'''(0)}{3!}x+...\; \; \; \; \; \; \; \; 18

From eq17,

p(0)=0\; \; \; \; \; \; 19

p'(0)=\frac{RT(1-bx)+bRTx}{(1-bx)^2}-2ax=RT\; \; \; \; \; \; \; 20

p''(0)=\frac{2b\left [ RT(1-bx)+bRTx \right ](1-bx)}{(1-bx)^4}-2a=2(bRT-a)\; \; \; \; \; \; \; 21

p'''(0)=\frac{6b^2RT}{(1-bx)^4}=6b^2RT\; \; \; \; \; \; \; 22

Substituting eq19 through eq22 in eq18 gives

p(x)=RTx\left [ 1+\left ( b-\frac{a}{RT} \right )x+b^2x^2+... \right ]\; \; \; \; \; \; \; \; 23

Substituting x=\frac{1}{V_m} back in eq23 yields

p(x)=\frac{RT}{V_m}\left [ 1+\frac{\left ( b-\frac{a}{RT} \right )}{V_m}+\frac{b^2}{V_m^{\: 2}}+... \right ]\; \; \; \; \; \; \; \; 24

Eq24 is the same as eq16 if B=\left ( b-\frac{a}{RT} \right ) and C = b2. If so, the coefficient C (and perhaps other higher coefficients) is not a function of temperature, which limits the accuracy of the equation in predicting the pressure of the real gas. Kamerlingh therefore decided to use experimental data to determine the coefficients B, C and so on, instead of using the van der Waals factors, resulting in eq16 as the final form rather than eq24.

Comparing eq16 and eq2, the compression factor is equal to the expansion part of the virial equation

Z=1+\frac{B}{V_m}+\frac{C}{V_m^{\: 2}}+...

If all the virial coefficients are equal to zero, Z = 1 and the virial equation becomes the ideal gas equation. For large Vm (i.e. at low pressures), all the terms with virial coefficients tend to zero with the virial equation transforming into the ideal gas equation again. The virial equation can also be expressed in terms of powers of pressure:

pV_m=RT\left ( 1+B'p+C'p^2+... \right )\; \; \; \; \; \; \; \; 25

The pressure version of the virial equation is constructed in a way that is consistent with the volume version, such that the equation becomes the ideal gas equation when all the virial coefficients are zero.

In summary, the virial equation’s accuracy in modeling the behaviour of real gases increases with increasing number of expansion terms. However, it may be cumbersome to determine the virial coefficients that are needed to make the equation work.

Previous article: van der Waal’s equation of state
Content page of real gases
Content page of intermediate chemistry
Main content page
Posted on

Chemical equilibrium: overview

Chemical equilibrium occurs when the rates of the forward and reverse reactions in a dynamic system become equal, resulting in constant concentrations of reactants and products despite ongoing processes.

Some chemical reactions are reversible (i.e. the products can react to re-form the reactants), e.g.

PCl_5(g)\rightleftharpoons PCl_3(g)+Cl_2(g)

Such reactions are denoted by the double harpoon sign \rightleftharpoons, instead of the single arrow sign → for irreversible reactions.

Consider only the presence of PCl5 in a closed, heated reaction vessel at the start of the reaction. Initially, PCl5 molecules collide with each other to form PCl3 and Cl2 at a relatively high rate, as both the temperature and the concentration of PCl5 are high. As some PCl3 and Cl2 are formed, they also begin to collide and re-form PCl5, but at a relatively slower rate. Over time, the decreasing concentration of PCl5 and the increasing concentrations of PCl3 and Cl2 reach a point where the forward reaction rate equals the reverse reaction rate, resulting in no net change in the concentrations of the reactant PCl5 and the products PCl3 and Cl2. We say that the reaction has attained dynamic equilibrium when it reaches such a state. The course of the reaction is represented by the graph below:

It is important to note that a closed system is necessary for a reaction to achieve chemical equilibrium.

 

Next article: Equilibrium constant
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

Units of the equilibrium constant

The thermodynamic definition of the equilibrium constant K (see this advanced level article for derivation) is

\Delta_rG^{\: o}=-RTlnK

where Δr Go is the reaction Gibbs energy at standard conditions (a constant for a particular reaction), R is the gas constant and T is temperature.

Since logarithms only take pure numbers, K is a dimensionless quantity. However, when equilibrium constants are calculated as a quotient of concentrations or partial pressures, the practice is to quote them in units of concentration or pressure according to the quotient.

K_c=\frac{\left [ C \right ]^p\left [ D \right ]^q...}{\left [ A \right ]^m\left [B \right ]^n...}\; \; \; or\; \; \; K_p=\frac{p_C^{ \; \; \; p}p_D^{ \; \; \;q}...}{p_A^{ \; \; \; m}p_B^{\; \; \; n}...}

For example, the units of Kc for

K_c=\frac{\left [ CoCl_4^{\; 2-} \right ]}{\left [ Co\left ( H_2O \right )_6^{\; 2+} \right ]\left [ Cl^- \right ]^4}

is mol-4dm12.

 

Next article: The relationship between Kp and Kc
Previous article: Equilibrium constant
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

Equilibrium constant

The equilibrium constant of a chemical reaction describes the relationship between the concentrations of the reactants and the concentrations of the products of the reaction at dynamic equilibrium.

Chemists found that when a reversible reaction reaches dynamic equilibrium, the product of the concentrations (or partial pressures) of the reaction products raised to the power of their stoichiometric coefficients divided by the product of the concentrations (or partial pressures) of the reactants raised to the power of their stoichiometric coefficients, has a constant value at a particular temperature (see this advanced level article for derivation). For the decomposition of PCl5 at 620K,

PCl_5(g)\rightleftharpoons PCl_3(g)+Cl_2(g)

we have

K_c=\frac{\left [ PCl_3 \right ]\left [ Cl_2 \right ]}{\left [ PCl_5 \right ]}

where [i] is the concentration in mol dm-3 of the species i.

We called this constant, Kc, the equilibrium constant. Since the species in this reaction are in the gaseous state and that the partial pressure of gas is proportional to its concentration, we can also express the equilibrium constant of this reaction in terms of partial pressures of the species:

K_p=\frac{P_{PCl_3}P_{Cl_2}}{P_{PCl_5}}

where pi is the partial pressure of gas i and Kp is the equilibrium constant in terms of partial pressures. Note that Kc may or may not be equal to Kp for a particular reaction (see here for details).

Another example is the reaction:

N_2(g)+3H_2(g)\rightleftharpoons 2NH_3(g)

where

K_c=\frac{\left [ NH_3 \right ]^2}{\left [ N_2 \right ]\left [ H_2 \right ]^3}\; \; \; or\; \; \; K_p=\frac{P_{NH_3}^{\; \; \; \; \; \; 2}}{P_{N_2}P_{H_2}^{\; \; \; \; 3}}

In general, for a reaction

mA+nB+...\rightleftharpoons pC+qD+...

K_c=\frac{\left [ C \right ]^p\left [ D \right ]^q...}{\left [ A \right ]^m\left [B \right ]^n...}\; \; \; or\; \; \; K_p=\frac{p_C^{ \; \; \; p}p_D^{ \; \; \;q}...}{p_A^{ \; \; \; m}p_B^{\; \; \; n}...}

 

Question

Calculate the equilibrium constant for the dissociation of PCl5 in a 250 ml vessel if the initial and equilibrium amounts of the reactant are 0.0175 mol and 0.0125 mol respectively (assuming no products formed initially).

Answer
PCl5 PCl3 Cl2

Initial conc, M

 0.0175/0.250 0 0

Equilibrium conc, M

 0.0125/0.250 (0.0175-0.0125)/0.250 (0.0175-0.0125)/0.250

K_c=\frac{\frac{0.0050}{0.250}\frac{0.0050}{0.250}}{\frac{0.0125}{0.250}}=8.0\times 10^{-3}\: M

 

 

Next article: Units of Equilibrium constant
Previous article: Overview
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

The relationship between \(K_c\) and \(K_p\)

What is the relationship between the equilibrium constant in terms of concentration \(K_c\) and the equilibrium constant in terms of partial pressure \(K_p\)?

For an ideal gas,

p=\frac{n}{V}RT\; \; \Rightarrow\; \; p=[concentration]RT\; \; \; \; \; \; \; \; 1

Substituting eq1 into the general equilibrium constant expression in terms of concentration gives:

K_c=\frac{[C]^p[D]^q...}{[A]^m[B]^n...}=\frac{\left ( \frac{p_C}{RT} \right )^p\left ( \frac{p_D}{RT} \right )^q...}{\left ( \frac{p_A}{RT} \right )^m\left ( \frac{p_B}{RT} \right )^n...}

which rearranges to:

(RT)^{(p+q+...)-(m+n+...)}K_c=\frac{p_C^{\; \; \; p}p_D^{\; \; \; q}...}{p_A^{\; \; \; m}p_B^{\; \; \; n}...}\; \; \; \; \; \; \; \; 2

Substituting the general equilibrium constant expression in terms of partial pressures, Kp, into eq2 yields:

K_p=K_c(RT)^{\Delta n}

where Δn = sum of stoichiometric coefficients of products – sum of stoichiometric coefficients of reactants.

Note that Kp = Kc if Δn = 0.

 

Next article: Why is water sometimes omitted from the equilibrium constant?
Previous article: Units of Equilibrium constant
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

Why is water sometimes omitted from the equilibrium constant?

Why is water sometimes omitted from the equilibrium constant? To answer this equation, we begin by noting that the equilibrium constants

K_c=\frac{[C]^p[D]^q...}{[A]^m[B]^n...}\; \; and\; \; K_p=\frac{p_C^{\; \;\; p}p_D^{\; \; \; q}...}{p_A^{\; \;\; m}p_B^{\; \;\; n}...}\; \; \; \; \; \; \; \; 3

are approximations of the thermodynamic definition of the equilibrium constant, which is:

K=\frac{a_C^{\; \;\; p}a_D^{\; \; \; q}...}{a_A^{\; \;\; m}a_B^{\; \;\; n}...}\; \; \; \; \; \; \; \; 4

where ai is the activity of species i.

For a dilute solution,

a_i=\frac{[i]}{[i]^o}\; \; \; \; \; \; \; \; 5

where [i]o is the concentration of the pure species at standard conditions of 1 bar and 298.15K.

For an ideal gas,

a_i=\frac{p_i}{p_i^{\: o}}\; \; \; \; \; \; \; \; 6

where pio is the pressure of the pure species at standard conditions of 1 bar and 298.15K.

Combining eq3 through eq6,

K_c=\frac{ \left (\frac{[C]}{[C] ^o} \right )^p\left (\frac{[D]}{[D] ^o} \right )^q...}{\left ( \frac{[A]}{[A]^o} \right )^m\left ( \frac{[B]}{[B]^o} \right )^n...}\; \; and\; \; K_p=\frac{ \left (\frac{P_C}{P_C^{\: o}} \right )^p\left (\frac{P_D}{P_D^{\: o}} \right )^q...}{\left ( \frac{P_A}{P_A^{\: o} }\right )^m\left ( \frac{P_B}{P_B^{\: o}} \right )^n...}\; \; \; \; \; \; \; \; 7

Consider the following reversible reaction:

CH_3COOH(l)+H_2O(l)\rightleftharpoons CH_3COO^-(aq)+H_3O^+(aq)

with

K_c=\frac{ \left (\frac{[CH_3COO^-]}{[CH_3COO^-] ^o} \right )\left (\frac{[H_3O^+]}{[H_3O^+] ^o} \right )}{\left ( \frac{[CH_3COOH]}{[CH_3COOH]^o} \right )\left ( \frac{[H_2O]}{[H_2O]^o} \right )}\; \; \; \; \; \; \; \; 8

Water, being in excess, is assumed to have a constant concentration throughout the reaction, approximately equal to that of its pure state. Hence \frac{\left [ H_2O \right ]}{\left [ H_2O \right ]^o}\approx1 and eq8 becomes

K_c=\frac{ \left (\frac{[CH_3COO^-]}{[CH_3COO^-] ^o} \right )\left (\frac{[H_3O^+]}{[H_3O^+] ^o} \right )}{\left ( \frac{[CH_3COOH]}{[CH_3COOH]^o} \right )}\; \; \; \; \; \; \; \; 9

Since the standard state of a solute is defined as 1 mol dm-3, eq9 approximates to

K_c=\frac{\left [ CH_3COO^- \right ]\left [ H_3O^+ \right ]}{\left [ CH_3COOH \right ]}\; \; \; \; \; \; \; \; 10

Therefore, water is excluded from the equilibrium constant if it acts as a solvent. However, for the reactions

CH_3COOH(l)+C_2H_5OH(l )\rightleftharpoons CH_3COOC_2H_5(l)+H_2O(l)

4HCl(g)+O_2(g)\rightleftharpoons 2H_2O(g)+2Cl_2(g)

water is not a solvent but a reactant, and the respective equilibrium constants are

K_c=\frac{\left [ CH_3COOC_2H_5 \right ]\left [ H_2O \right ]}{\left [ CH_3COOH \right ]\left [ C_2H_5OH \right ]}

K_c=\frac{\left [ H_2O \right ]^2\left [Cl_2 \right ]^2}{\left [ HCl \right ]^4\left [O_2 \right ]}

In the case of a reversible reaction containing one or more solid species, e.g.,

HCl(g)+LiH(s)\rightleftharpoons LICl(s)+H_2(g)

the concentrations of the solid compounds are assumed to be the same as that of their respective pure states. Hence,

K_c=\frac{\left [ H_2 \right ]}{\left [HCl\right ]}\; \; or\; \; K_p=\frac{p_{H_2}}{p_{HCl}}

 

Question

Write the equilibrium constants for the following reactions:

a) CaCO_3(s)\rightleftharpoons CaO(s)+CO_2(g)

b) CH_3COOC_2H_5(l)+H_2O(l)\rightleftharpoons CH_3COOH(l)+C_2H_5OH(l)

c) Co(H_2O)_6^{\; 2+}(aq)+4Cl^-(aq)\rightleftharpoons CoCl_4^{\; 2-}(aq)+6H_2O(l)

Answer

a) K_p=p_{CO_2}

b) K_c=\frac{\left [ CH_3COOH \right ]\left [ C_2H_5OH \right ]}{\left [ CH_3COOC_2H_5 \right ]\left [ H_2O \right ]}

H2O is not a solvent in the hydrolysis reaction but a reactant. A typical ester hydrolysis reaction involves adding, for example, 0.10 M of CH3COOC2H5, 0.10 M of H2O and a catalyst in an inert organic solvent.

c) K_c=\frac{\left [ CoCl_4^{\; \; 2-} \right ]}{\left [ Co(H_2O)_6^{\; \; 2+} \right ]\left [ Cl^- \right ]^4}

The reaction occurs in an aqueous solution, i.e., the solvent is water.

 

Next article: Ion-product constant for water
Previous article: The relationship between Kp and Kc
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

Ion-product constant for water

The ion-product constant for water describes the relationship between molecular water and its dissociated ionic components at dynamic equilibrium.

Pure water dissociates partially to give the hydroxonium and hydroxide ions.

2H_2O(l)\rightleftharpoons H_3O^+(aq)+OH^-(aq)

Since water is the solvent, its activity approximately equals to one and the equilibrium constant is

K_w=\left [ H_3O^+ \right ]\left [ OH^- \right ]\; \; \; \; \; \; \; \; 11

Kw is called the ion-product constant for water. Conductivity measurements of pure water reveals that [H3O+] = 10-7 M at 25oC. Since the concentration of hydroxonium ions and hydroxide ions are formed only from the dissociation of water molecules, [H3O+] = [OH–], giving Kw = 10-14 M at 25oC . It is important to note that Kw remains equal to 10-14 M at 25oC, regardless of whether the H3O+ and OH– ions originate from water or from added acids or bases.

 

Question

What is the concentration of OH– when HCl is added to water at 25oC to give a pH of 2?

Answer

According to Le Chatelier’s principle, the increased [H3O+] shifts the position of the equilibrium of eq11 to the left to attain a new equilibrium where

[OH^-]=\frac{10^{-14}}{10^{-2}}=10^{-12}\: M

 

 

Next article: Acid/base dissociation constant
Previous article: Why is water sometimes omitted from the equilibrium constant?
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

Distribution coefficient (partition coefficient)

The distribution coefficient describes the relative concentrations of a chemical compound in two immiscible solvents.

When a solute, X, with different solubilities in two immiscible solvents, e.g., water and hexane, is shaken in a separating funnel containing both solvents and left to settle, a dynamic equilibrium is established such that the rate of the solute moving from the aqueous layer to the organic layer is the same as the rate of the solute moving from the organic layer to the aqueous layer.

X(aq)\rightleftharpoons X(org)

The equilibrium constant, called the distribution coefficient (or partition coefficient) is given by:

K_d=\frac{[X(org)]}{[X(aq)]}

If the compound is more soluble in the organic phase, the distribution coefficient will be greater than 1. If it is more soluble in the aqueous phase, the coefficient will be less than 1. This coefficient is important in various fields, like pharmacology, where it helps predict how a drug will behave in the body (its absorption, distribution, and excretion), and in environmental science, where it can indicate how a pollutant might move between water and soil.

 

Question

10.00 g of benzoic acid that is dissolved in 100 ml of water is shaken with 50 ml of chloroform and left to settle. 20 ml is then extracted from the aqueous layer and titrated with 6.40 ml of 0.1000 M of NaOH. Calculate the distribution coefficient for benzoic acid in the two solvents.

Answer

C_6H_5COOH(l)+NaOH(aq)\rightarrow C_6H_5COO^-Na^+(aq)+H_2O(l)

K_d=\frac{\frac{\frac{10.00}{122.05}-(0.1000\times 0.00064\times 5)}{0.05}}{\frac{0.1000\times 0.0064\times 5}{0.1}}=49.2

 

Next article: Le Chatelier’s principle
Previous article: Solubility product
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

Le Chatelier’s principle

Henry Louis Le Chatelier, a French chemist, developed a principle of chemical equilibrium in the late 1800s, which states:

A change in concentration, pressure or temperature to a system at dynamic equilibrium causes the position of the equilibrium to shift in the direction that minimises the change.

The principle is based on the thermodynamic properties of the equilibrium constant, which is dependent only on temperature for a particular reaction. Let’s see how the factors (concentration, pressure and temperature) affect the equilibria of chemical reactions in the next few articles.

 

Next article: Effect of concentration on equilibrium
Previous article: Distribution coefficient (partition coefficient)
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Posted on

Solubility product

The solubility product of a chemical compound is the equilibrium constant for the dissolution of the compound in its solid state in an aqueous solution.

The solubility of a solute is the maximum amount of the solute in grammes that can dissolve in a 100 ml (or sometimes 1 dm3 or 1 kg) of a solvent at a particular temperature. For example, the solubility of AgCl in 100 ml of water at 25oC is about 1.92×10-4 g or 1.34×10-5 moles.

To illustrate the concept of solubility product, let’s begin by adding 1.0×10-5 moles of solid AgCl in 100 ml of water at 25oC. The solid completely dissolves, producing 1.0×10-5 moles each of Ag+ and Cl– ions. As we increase the amount of solid AgCl to 1.34×10-5 moles, it still dissolves completely, yielding the maximum concentration of Ag+ and Cl– ions possible in 100ml of water. At this point, the solution is considered saturated. If we add more than 1.34×10-5 moles of AgCl, any excess solid will remain undissolved. The concentrations of Ag+ and Cl– ions stay constant at 1.34×10-5 mol per 100 ml, and the system reaches equilibrium. At equilibrium, the rate at which solid AgCl dissolves into ions equals the rate at which the ions recombine to form the solid, establishing a dynamic balance:

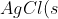AgCl(s)\rightleftharpoons Ag^+(aq)+Cl^-(aq)

Since the concentration of solid silver chloride is assumed to be the same as that of its pure state, the equilibrium constant is:

K_{sp}=[Ag^+][Cl^-]

with

Ksp being the solubility product of AgCl, which is 1.8×10-10 at 25oC.
[Ag+] is the maximum amount of Ag+ in 100 ml of water.
[Cl–] is the maximum amount of Cl– in 100 ml of water.

The solubility product of AgCl is therefore the mathematical product of the solubility of Ag+ (with respect to Cl–) and the solubility of Cl– (with respect to Ag+) raised to the power of their respective stoichiometric coefficients in 100 ml of solvent at a particular temperature. In general, the solubility product of AxBy is

K_{sp,A_xB_y}=[A^{y+}]^x[B^{x-}]^y

 

Question

Calculate the Ksp for PbCl2, given that its solubility is 0.0108 g/ml at 20oC.

Answer

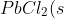PbCl_2(s)\rightleftharpoons Pb^{2+}(aq)+2Cl^-(aq)

Solubility of Pb2+ with respect to Cl– = \frac{10.8}{\left [ 207.2+\left ( 2\times 35.45 \right ) \right ]}\; mol\, dm^{-3}

Solubility of Cl– with respect to Pb2+ = \frac{2\times 10.8}{\left [ 207.2+\left ( 2\times 35.45 \right ) \right ]}\; mol\, dm^{-3}

K_{sp}=\left [ Pb^{2+} \right ]\left [ Cl^- \right ]^2=\left ( \frac{10.8}{278.1} \right )\left ( \frac{2\times 10.8}{278.1} \right )^2=2.3\times 10^{-4}\; mol^{\: 3}\, dm^{-9}

 

Question

Some solid Na2CO3 is slowly added to a solution containing 0.020 M of Zn2+ and 0.020 M of Ag+. Given that Ksp(ZnCO3) = 1.46 x 10-10 and Ksp(Ag2CO3) = 8.46 x 10-12, which cation will be precipitated first? What is the concentration of this cation in the solution when the other cation starts to precipitate?

Answer

[CO32-] required to begin Ag2CO3 precipitation is:

[CO32-] required to begin ZnCO3 precipitation is:

Therefore, Zn2+ will be precipitated first. When Ag2CO3 starts to precipitate,

 

Just as Ka and Kb are only useful for comparing weak acids and weak bases respectively, Ksp is only useful for comparing sparing soluble salts, as highly soluble salts have a higher probability of forming ion pairs. An ion pair consists of a cation and an anion that are electrostatically attracted to each other, rather than being individually surrounded by solvent molecules. This interaction alters their physical properties—for example, their mobility—and can distort the measurement of ion concentrations in solution when using ionic or conductivity methods. As a result, the accuracy of the Ksp value may be compromised. In general, the higher the solubility of a solid, the greater the concentration of ions in the solvent, which increases the likelihood of ion pair formation.

Furthermore, just as Kw is constant at a particular temperature regardless of the source of H3O+ and OH–, Ksp for a solid remains constant at a particular temperature regardless of the source of the dissolved ions. For example, the presence of NaCl in a saturated solution of AgCl causes the latter to precipitate, as Cl– is common to both species. The decrease in the solubility of a dissolved compound in the presence of an ion in common with the dissolved compound is called the common ion effect.

 

Question

Is Ksp dependent on the volume of the solution?

Answer

No. is a thermodynamic equilibrium constant that is governed by the formula

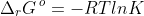
\Delta_rG^{\: o}=-RTlnK

Hence, Ksp is only dependent on temperature. If we dilute a solution of PbCl2 that is in equilibrium with solid PbCl2, the increase in volume of the solution shifts the position of the equilibrium according to Le Chatelier’s principle to produce more aqueous Pb2+ and Cl– such that the saturation concentrations (mole per volume) of Pb2+ and Cl– remains unchanged when the new equilibrium is attained.

Another way to look at it is that Ksp is the mathematical product of the solubility of the ions of a compound, raised to the power of their respective stoichiometric coefficients in a particular volume of solvent at a particular temperature. Since solubility is an intensive property, Ksp is independent of the volume of solvent.

 

Next article: Distribution coefficient (partition coefficient)
Previous article: Acid/base dissociation constant
Content page of chemical equilibrium
Content page of intermediate chemistry
Main content page
Mono Quiz