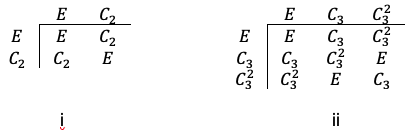The degrees of freedom of a chemical species are the number of independent displacements of the species.
An atom has three degrees of freedom because its instantaneous displacement is defined by three orthogonal directions in the space. A molecule of
atoms is characterised by
degrees of freedom, as every atom can be displaced from its equilibrium position in three orthogonal directions. Each of the
motion is independent and cannot be expressed as a combination of the others. However, the presence of chemical bonds restrict some of these displacements, resulting in three groups of independent motion: translation, rotation and vibration.

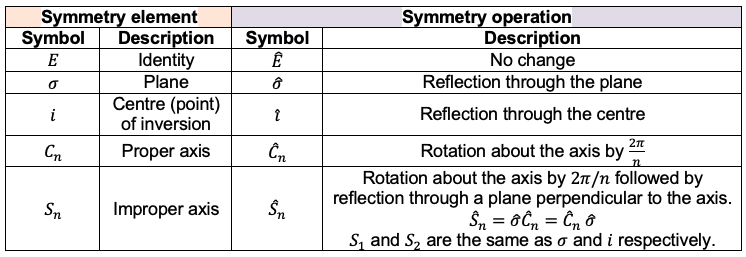
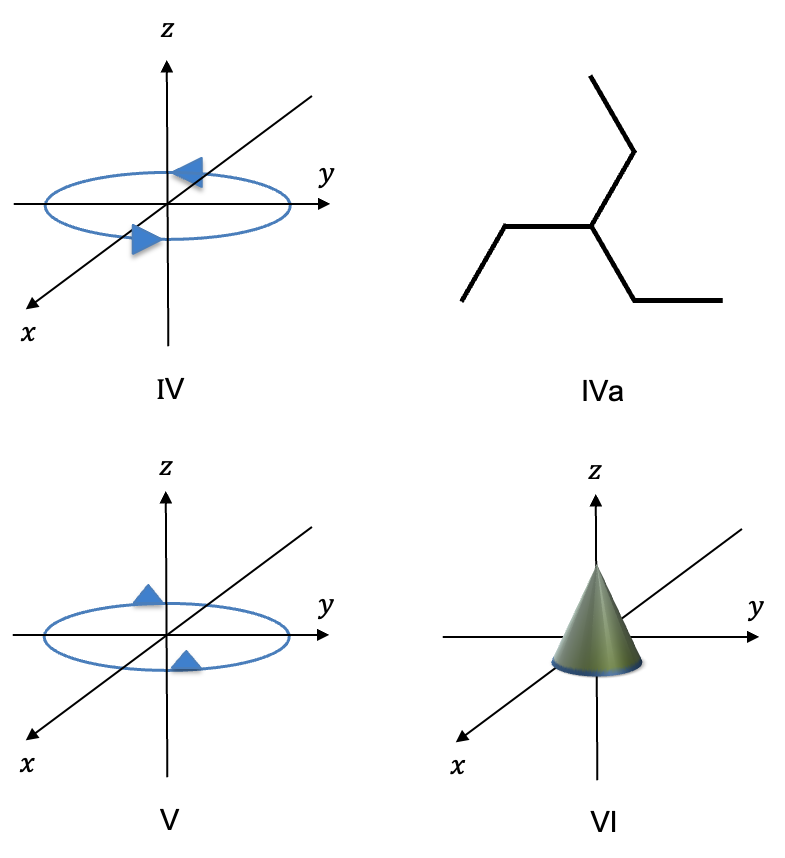
To understand how the restriction of molecular motion by chemical bonds results in three groups of motion, each of which is independent of the others, we consider a diatomic molecule (see diagram above), where the red, purple and brown arrows represent instantaneous displacements of the atoms.
Firstly, we would expect the molecule to have six degrees of freedom since . Next, the motion of the two atoms (red arrows) in the same direction and with the same magnitude, which is equivalent to the motion of the centre of mass of the molecule in the positive
-direction, is a translational motion. Similarly, the centre of mass of the molecule can move independently in the
-direction and
-direction, resulting in another two degrees of translational freedom.
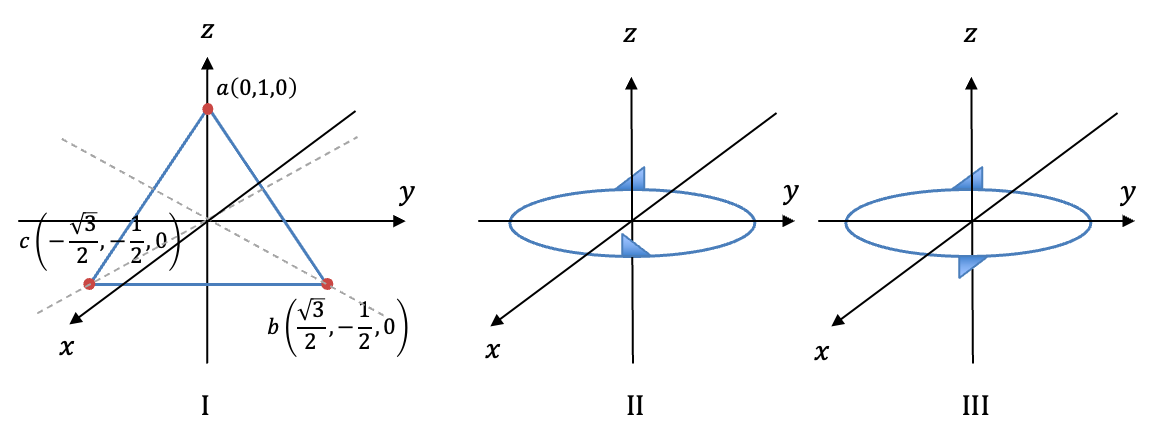
The rotational motion of the molecule around the -axis passing through its centre of mass is described by the two brown arrows that are tangent to the circle of motion. The rotation about the
-axis contributes to another degree of freedom. However, the molecule spinning around the
-axis is not considered a degree of freedom, as no atomic displacement has occurred. In fact, all linear molecules have two degrees of rotational freedom. One common property of translational motion and rotational motion is that they are both rigid transformations, meaning that the bond length doesn’t change throughout either motion.
When the atoms are displaced in opposite directions (purple arrows), they oscillate about their equilibrium positions because they are restricted by the chemical bond. This is known as vibrational motion.
Combining two degrees of rotational freedom with three degrees of translational freedom, all linear molecules have degrees of vibrational freedom. Since the centre of mass moves during translation, while the position of the centre of mass of a molecule does not change during rotational motion and vibrational motion, translational motion is independent of rotational motion and vibrational motion. Furthermore, rotational motion is independent of vibrational motion because rotational motion is a rigid transformation, whereas vibrational motion is not. In general, the three types of motion are independent of one another and all possible motion of atoms of a molecule are a combination of them.

Question
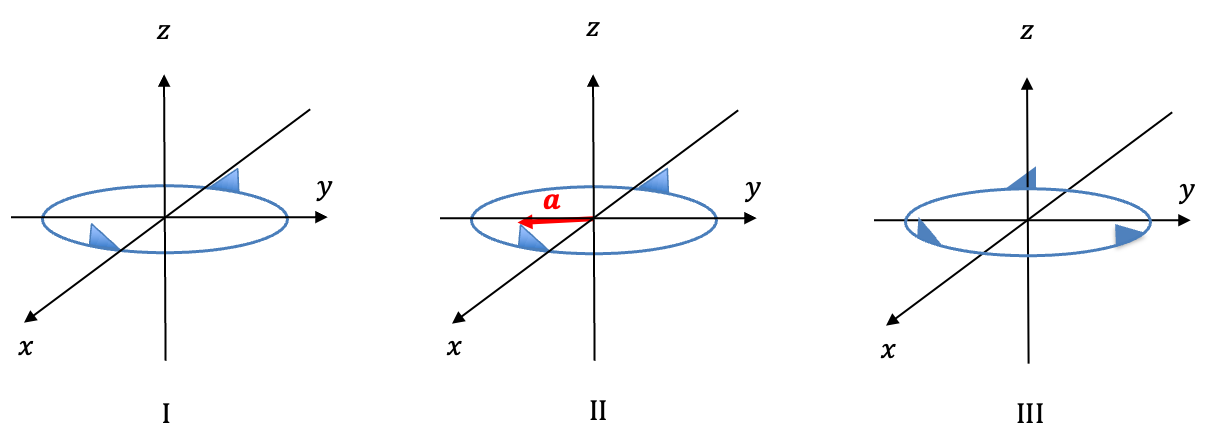
What if the brown arrows represent linear motions, instead of tangents to the circle of motion?
Answer
If that’s the case, the atoms move linearly in the directions of the arrows until they are restricted by the chemical bond. Such a motion is a combination of vibrational and rotational motions and not an independent motion. Therefore, it is not a degree of freedom.
Since an arrow on an atom can be expressed as a linear combination of three orthogonal vectors centred on the atom, the degrees of freedom of a molecule with atoms are often expressed in terms of
orthogonal unit displacement vectors.

For example, when the motion of the water molecule in the above diagram is described only by the three -unit vectors, and the magnitudes of the displacement of all atoms are equal, the molecule is translating in the
-direction. Similarly, if the only unit vectors describing the molecule’s motion are
and
, and the atoms have equal displacement magnitude, the molecule is rotating around the
-axis. We will show, in the next article, that the translational motion of
in the
-direction and the rotational motion of
around the
-axis can be expressed as the symmetry-adapted linear combinations
and
respectively.
and
can also describe a twisting motion of the molecule (like a gym glider machine). However, such a motion, as explained in the Q&A above, is not a degree of freedom of the molecule. Unlike a linear molecule, a non-linear molecule has three rotational degrees of freedom, and hence,
degrees of vibrational freedom. Group theory allows us to determine which irreducible representation of a point group a particular degree of freedom belongs to, and consequently provides a simple way to predict spectroscopic properties the molecule.