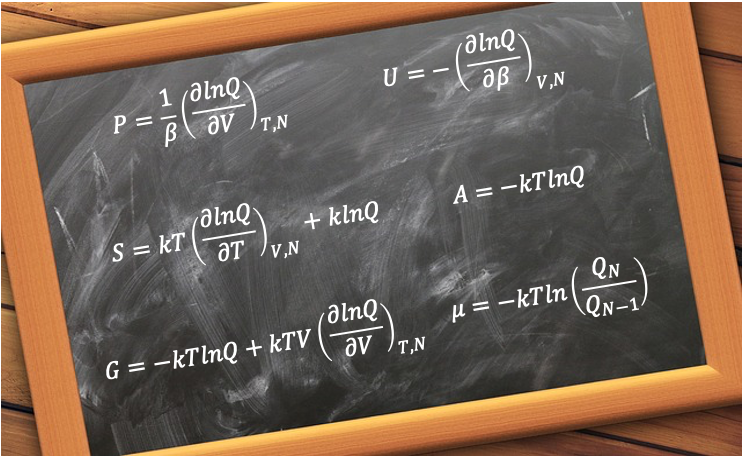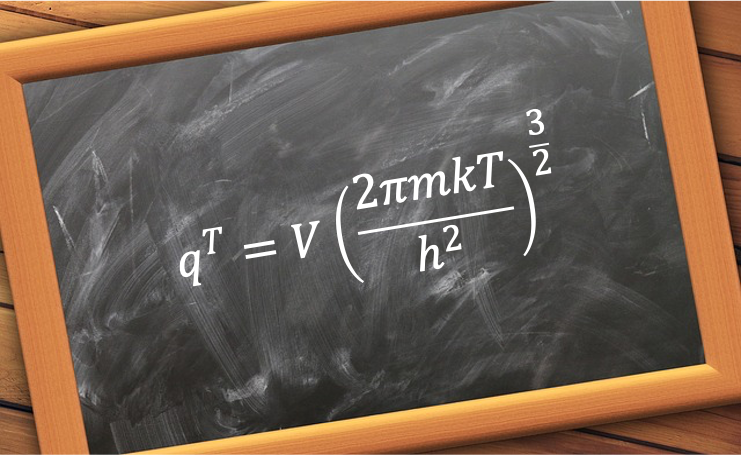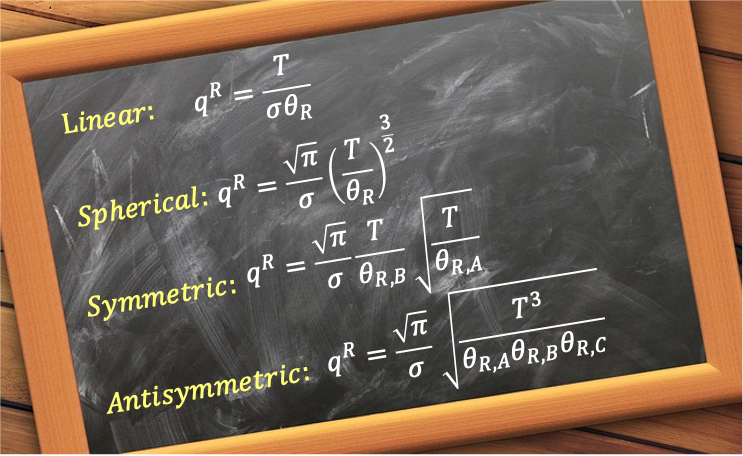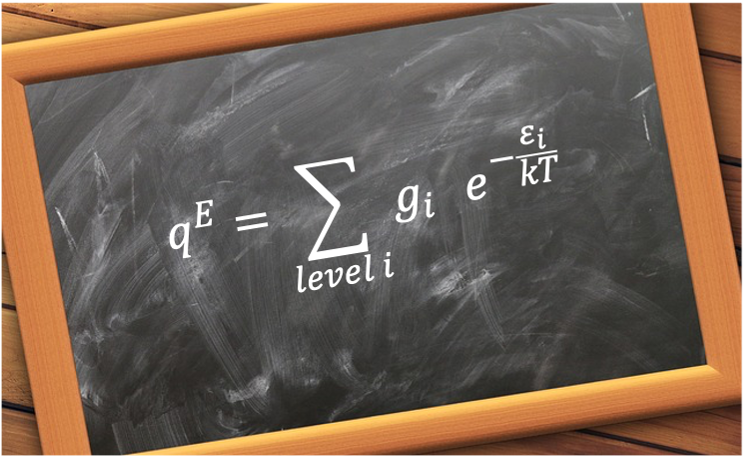Vibration-rotation spectra arise from the simultaneous vibrational and rotational transitions of molecules, typically observed in the infrared (IR) region of the electromagnetic spectrum. These spectra provide detailed information about molecular structure, bond strength, and moment of inertia.
For a molecule to be IR active, it must have a permanent dipole or a dipole moment that changes over time. Homonuclear diatomic molecules, such as O2, lack these properties and are therefore IR inactive. In contrast, when a heteronuclear diatomic molecule absorbs IR radiation, it can undergo a change in its vibrational energy level along with a change in its rotational state, resulting in a distinctive pattern of spectral lines. These energy levels (expressed in wavenumbers), characterised by the rigid rotor–harmonic oscillator approximation, are the sum of its allowed rotational and vibrational energies:
The selection rules governing transitions are given by eq7:
However, the condition applies only to molecules with a nonzero projection of the electronic orbital angular momentum onto the internuclear axis (i.e.
), such as NO. To elaborate, the rotational quantum number
represents the magnitude of the coupled total angular momentum vector, given by
where:
is the nuclear rotation angular momentum (end-over-end rotation).
is the electronic orbital angular momentum.
is the vibrational angular momentum.
is the electronic spin angular momentum.
Note: Nuclear spin angular momentum is excluded because it couples only weakly to the other components.

Question
What is the relationship between the component vectors of and their corresponding quantum numbers?
Answer
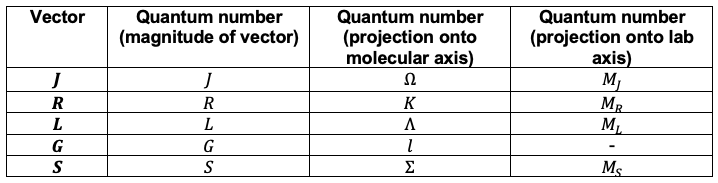
Note: The spin quantum number should not be confused with the electronic state
.
The selection rules for a pure vibrational transition are , while those for pure rotational transitions (ignoring the
-related fine structure transitions, which are often unresolved in most experimental spectra) are
. Additionally, the total angular momentum
of the system must be conserved during a photon-mediated transition, as a photon carries one unit of angular momentum.
For a closed shell heteronuclear diatomic molecule like HCl ( ),
, with
. Therefore, the absorption of the IR photon’s angular momentum during
must be accounted for by
, resulting in
.

Conversely, the ground state of NO () has an unpaired electron in a degenerate
molecular orbital, giving
,
,
. This allows the coupling (vector addition) of
and
to reorient internally in such a way that it can exactly compensate for the photon’s angular momentum (see diagram above). In other words,
can be preserved without changing
, making the transitions
, where
, no longer forbidden.
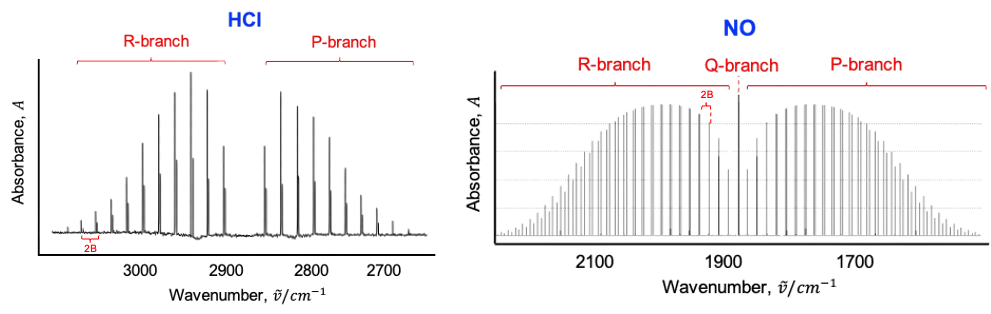
In general, the absorption lines in a vibration-rotation spectrum can be grouped into three types, called branches (see diagram below). The R branch consists of all transitions, with energies given by:
where .
transitions form the P branch, with energies:
where .
The energy separation between adjacent lines in the P and R branches corresponds to . Therefore, the vibration-rotation spectrum, like the pure rotation spectrum, allows the moment of inertia and bond length of molecules to be calculated. The relative intensities of the lines in the P and R branches depend on the product of
and
, the same mechanism that governs the intensities in a pure rotational spectrum.

Question
According to the above diagram, the rotational constant is smaller for NO than for HCl. Why?
Answer
The rotational constant is given by , where
. Since the reduced mass
of HCl is smaller than that of NO,
.
Finally, the Q branch, if allowed by selection rules, consists of transitions, all of which have the same energy:
This means that transitions such as and
appear as a single line in the spectrum under the rigid rotor-harmonic oscillator approximation. In reality, the Q branch appears as a series of closely spaced lines rather than a single line. This is because
changes with the vibrational quantum number
, where the bond length
increases slightly in higher vibrational states, causing the moment of inertia
to increase and
to decrease. From eq9,
Eq14 shows that transitions such as and
now appear as separate lines. Since
, the spacing between these lines decreases with
. At lower resolution, these closely spaced lines give the Q-branch the characteristic appearance of a single, strong, broad peak.
Using the same logic,
which rearranges to:
As the spacing between the lines of the R-branch decreases slightly as
increases.

Question
Is the change in at higher
the same as centrifugal distortion?
Answer
No, it is different from centrifugal distortion. When a molecule vibrates at higher , the average bond length increases slightly. This is purely a vibrational effect. In contrast, centrifugal distortion is a rotational effect, which also causes the bond to stretch slightly as the rotational speed increases at higher
. In other words, the former phenomenon depends on
, while the latter depends on
. If centrifugal distortion in considered, eq9 becomes
and
For the P-branch,
Since the third term on RHS of eq16 is negative, the lines of the P-branch diverge slightly as increases. Note that eq14, eq15 and eq16 reduce to eq13, eq11 and eq12 respectively if
.

Question
Why do many IR spectra have broad, continuous peaks rather than discrete lines?
Answer
Many common IR spectra are taken in the liquid phase (or solid), which leads to broadened, continuous-looking peaks. In the liquid or solid phase, molecules interact strongly with each other via van der Waals forces and hydrogen bonding. These interactions distort the the dipole moments of molecules and broaden energy levels. On the other hand, intermolecular forces are minimal in dilute samples of gaseous molecules. When these gas-phase samples are analysed with high-resolution instruments, discrete peaks — especially rotational fine structure — can be observed.