Category: Intermediate Chemistry

Mass–energy equivalence is the principle that mass can be converted into energy and energy into mass, with the relationship quantified by E = mc².

The idea of mass–energy equivalence emerged from attempts to resolve inconsistencies between classical physics and electromagnetism in the early 20th century. Before Einstein, physics treated mass and energy as completely separate quantities: mass was seen as “matter content,” while energy was something objects had due to motion, heat or fields. However, developments in electromagnetism (especially Maxwell’s equations) and experiments with light showed that energy itself carries momentum, hinting that energy and mass might be more deeply connected.

In 1905, Albert Einstein published his special relativity paper and later that year derived a key consequence: if an object emits energy (like light), its mass must decrease by an amount proportional to the energy released divided by the speed of light squared. This led to the compact relation , where is the speed of light. Later experiments in nuclear physics confirmed the idea dramatically: in processes like nuclear fission and fusion, small losses of mass are converted into enormous amounts of energy, matching Einstein’s equation with high precision.

To derive the relation, we refer to Einstein’s thought experiment, which uses the principles of conservation of momentum and conservation of the centre of mass. Consider a hollow, completely closed box of mass and length , floating at rest in deep, frictionless space. Suppose a photon of energy is spontaneously emitted from the left wall towards the right wall (see diagram below). The momentum of the photon is given by , which can be derived by substituting and de Broglie’s relation into Planck’s law .

According the law of conservation of momentum, the emission of the photon causes the box to recoil to the left with velocity and momentum . It follows that , or equivalently,

As the photon travels across the box and strikes the right wall, it transfers its momentum back to the box, bringing the box to rest again. Thus, the box starts at rest and ends at rest, but during the photon’s transit it shifts leftwards by a very small distance , where is the time taken for the photon to travel across the box. Hence,

Substituting eq20 and eq21 into gives:

Since no external force acts on the system, the centre of mass must remain stationary. To resolve the apparent contradiction caused by the box’s displacement, Einstein concluded that the energy carried by the photon must possess an inertial equivalent mass from the left side of the box to the right side. The shift in the photon’s equivalent mass balances the displacement of the box:

Substituting eq22 into eq23 and rearranging yields the Einstein relation:

This result is not limited to photons, since the photon merely serves as a convenient carrier of energy across the box. Einstein’s thought experiment considers the box-photon system as a whole in its rest frame. Before the photon is emitted and after it is absorbed, the total system remains stationary. While the photon itself moves within the box, its energy remains part of the total energy of the closed system. The moving photon therefore contributes to the system’s total rest mass according to . In other words, the equation applies to the total energy contained in a system that is overall at rest, even if energy is moving internally within that system. It demonstrates a more general principle: any form of energy possesses inertia and therefore contributes to the rest mass of a system. For example, a heated object possesses slightly greater mass than the same object when colder. In this case, refers to the total rest mass of the entire object as a system, including both the masses of its constituent particles and their internal energy. The hotter object contains additional thermal energy associated with the motion and interactions of its particles, so its total mass is slightly greater. The energy difference between the hotter and cooler object is therefore given by .

 

 

 

previous article: Nuclear binding energy per nucleon

Content page of mass in chemistry

Content page of intermediate chemistry

Main content page

Photoelectron Spectroscopy (PES) is an analytical technique that measures the kinetic energies of electrons emitted from a substance when it is irradiated with electromagnetic radiation, revealing information about the substance’s electronic structure and composition.

This technique is based on the photoelectric effect, in which photons striking either isolated gas-phase atoms or the surface of a solid material eject electrons. By measuring the kinetic energy () of the emitted electrons for a given incident photon frequency , scientists can calculate their ionisation energies (also known as binding energy) using the equation:

where

is the photon energy ( is the Planck’s constant).
is the measured kinetic energy of the -th emitted electron of mass and velocity .
is the ionisation energy of the -th electron. According to Koopmans’ theorem, this value is approximately equal to the negative of the energy of the occupied atomic or molecular orbital from which the electron was removed.

In atoms, electrons closer to the nucleus have higher ionisation energies because they experience stronger electrostatic attraction to the nucleus. As a result, their measured kinetic energies produce characteristic peaks in the photoelectron spectrum corresponding to the orbital energies, with core orbitals such as 1s appearing at much higher ionisation energies than outer orbitals such as 2s or 2p. By analysing the positions of these peaks, the energies of individual atomic orbitals can be determined.

 

 

Similarly, PES is useful in studying molecular orbitals. When a molecule is irradiated, electrons are removed from bonding, nonbonding or antibonding molecular orbitals. Each molecular orbital gives rise to a separate peak in the spectrum. The first peak in a molecular PES spectrum usually corresponds to the highest occupied molecular orbital (HOMO), since these electrons require the least energy to remove. Peaks at higher ionisation energies correspond to lower-energy occupied orbitals. By comparing the experimental spectrum with theoretical calculations (e.g. using the Hartree-Fock method), chemists can identify the nature and ordering of molecular orbitals. PES therefore provides valuable information about electronic structure, chemical bonding, orbital energies and the stability of atoms and molecules.

Generally, there are two main types of PES:

• • Ultraviolet Photoelectron Spectroscopy (UPS) — uses ultraviolet light to study valence electrons and chemical bonding.
  • X-ray Photoelectron Spectroscopy (XPS) — uses X-rays to analyse elemental composition and oxidation states.

A typical photoelectron spectrometer (see above diagram) comprises of the following parts:

1. 1. Radiation Source: It provides photons of known energy to irradiate the sample.
      • In UPS, ultraviolet lamps such as helium discharge lamps are commonly used. The lamp contains low-pressure He gas and two electrodes connected to a high-voltage power supply. When a sufficiently large potential difference is applied across the electrodes, the gas becomes ionised, and the accelerated electrons collide with He atoms, exciting their electrons to higher energy levels. As the excited He atoms relax back to lower energy states, they emit characteristic ultraviolet radiation. The most commonly used emission lines are He I (21.2 eV) and He II (40.8 eV).
      • In XPS, X-ray sources, such as radiation, are employed. The radiation is generated in an X-ray tube, which consists of a hot tungsten filament (cathode) that emits electrons. These electrons are then accelerated towards a metal anode (e.g. Mg) by applying a large potential difference between electrodes. For , the applied voltage allows the accelerated electrons to gain sufficient kinetic energy to eject an (–shell) electron from the anode. Subsequently an (-shell) electron drops to the shell to fill the vacancy, emitting the characteristic 1253.6 eV radiation. Depending on the experiment, other metal anodes may also be used with different accelerating potentials to produce X-rays of different energies (e.g. or ).
   2. Sample Chamber: The sample is placed inside an ultra-high vacuum chamber to prevent emitted electrons from colliding with air molecules. The vacuum also keeps the sample surface clean and uncontaminated. The chamber contains openings that allow the incident radiation to enter and the emitted electrons to pass into the energy analyser.
   3. Energy Analyser: This consists of electrostatically charged plates shaped into hemispheres that deflect the paths of the electrons exiting the sample chamber according to their velocities. Only electrons with a specific kinetic energy follow the correct curved trajectory that allows them to pass through the analyser and reach the detector. Electrons with kinetic energies that are too high or too low are deflected either too little or too strongly and therefore collide with the analyser walls instead of reaching the detector. By varying the potential difference between the hemispherical plates, the analyser selectively allows electrons of different kinetic energies to reach the detector.
   4. Detector: The detector, such as microchannel plates (MCPs), records the number of electrons transmitted by the analyser at different kinetic energies. An MCP is a thin glass disk riddled with millions of microscopic tubes called channels. An incoming photoelectron enters a channel and collides with its resistive glass wall, which is coated with a material that emits 2–3 secondary electrons each time it is struck. However, this small number of electrons is insufficient to generate an appreciable signal. Therefore, the secondary electrons are accelerated further down the channel by an applied electric potential, causing repeated collisions with the channel walls and producing an electron cascade. By the time the cascade reaches the end of the channel, a single incoming electron has been amplified into a measurable pulse of electrons. The resulting electrical signal is then collected and counted by the detector electronics. By repeatedly varying the potential difference between the hemispherical plates over a range of energies and recording the corresponding detector signal, a photoelectron spectrum is produced.

The vertical axis of a typical photoelectron spectrum corresponds to the relative number of electrons (peak intensity), while the horizontal axis may be labelled “ionisation energy” or “binding energy”. Unlike ionisation energy scales, binding energy scales are often plotted in reverse (with high energy on the left and lower energy on the right). Photoelectron spectra in high school textbooks are usually simplified and depicted with isolated peaks. For example,  the photoelectron spectrum of nitrogen consists of three peaks corresponding to electrons residing in the 1s, 2s and 2p orbitals, while that of sodium has four peaks (see diagram below).

In reality, a sample of nitrogen exists primarily as diatomic N₂​ molecules rather than isolated atoms. As a result, the observed photoelectron spectrum is more complex than the simplified atomic representation shown in introductory treatments. In molecular systems, atomic orbitals combine to form molecular orbitals, and electrons are removed from these molecular orbitals during photoionisation. Consequently, the spectrum of N₂​ contains peaks associated with bonding and antibonding molecular orbitals rather than purely atomic 1s, 2s, and 2p orbitals (see diagram below).

In addition, real photoelectron spectra are affected by several other factors, including spin–orbit splitting, vibrational fine structure, instrumental resolution, and interactions between emitted electrons and neighbouring atoms. Therefore, experimentally obtained spectra often display broadened or overlapping peaks instead of perfectly sharp lines.

Similarly, a sample of sodium consists of sodium crystals instead of isolated atoms. In the solid state, the outer 3s electrons are not confined to individual sodium atoms but become delocalised throughout the crystal lattice, forming electronic bands. As a result, the photoelectron spectrum of metallic sodium differs from the simplified atomic spectrum typically presented in introductory discussions. Instead of discrete atomic energy levels alone, the spectrum reflects the band structure of the solid, including the partially filled valence band formed by the 3s electrons. Consequently, experimentally measured spectra of sodium metal often exhibit broadened features and additional fine structure arising from interactions between neighbouring atoms in the crystal lattice.

Despite these complexities, simplified spectra remain useful for introducing the relationship between electron configuration and binding energy.

 

 

One important application of PES is the analysis of semiconductors. Semiconductors function because of the gap between the valence band (where electrons are bound) and the conduction band (where electrons can move freely and conduct electricity). PES is uniquely suited to map these regions, where lower-energy UV photons in UPS eject electrons from the valence band. As a result, the Fermi Level E_F can be measured relatively to the top of the valence band (see diagram above).

In an n-type semiconductor, the Fermi level shifts closer to the conduction band, whereas in a p-type semiconductor, it shifts closer to the valence band. PES can detect these shifts with high precision, allowing verification of whether the doping process was successful (see diagram above). In addition, higher-energy X-rays in XPS eject tightly bound core electrons, helping to identify the elements present in a semiconductor because each element has characteristic core-electron binding energies. Small shifts in these binding energies also reveal the chemical environment of the atoms, such as their oxidation states or the types of chemical bonds they form. This enables scientists to determine the composition of dopants, surface oxides, and other impurities in the semiconductor material (see diagram below, where carbon is an impurity and arsenic is a dopant). Therefore, PES serves as a powerful tool for analysing both the electronic structure and chemical composition of semiconductors.

 

Previous article: Infrared spectroscopy

Content page of UV-vis and IR spectroscopy

Content page of intermediate chemistry

The Michaelis–Menten equation describes how the rate of an enzyme-catalysed reaction increases with substrate concentration and eventually plateaus at a maximum value () due to enzyme saturation.

Consider an enzyme binding reversibly to a substrate to form the Michaelis complex , which then produces product(s) and regenerates the enzyme:

where , and are rate constants.

The rate of formation and breakdown of is given by:

Let’s assume:

1. 1. The initial rate method is used to measure the reaction.
   2. The initial substrate concentration is much greater than the initial enzyme concentration , so that the free substrate concentration is approximately equal to .
   3. Initial product formation is negligible and the step is irreversible.
   4. Total enzyme concentration is conserved: .

Therefore, the enzyme–substrate complex builds up rapidly during an initial transient phase and then reaches a constant concentration (see diagram above). During this period, . This is known as the steady-state approximation, with

where is the Michaelis constant.

Substituting into eq80 gives:

which rearranges to:

Since ,

Because product formation is relatively slow initially, becomes the rate determining step, with the initial reaction velocity of the overall reaction being:

Substituting eq81 into eq82 yields the Michaelis-Menten equation:

where is a constant for a fixed .

When , we have (see above diagram). In other words, the rate of the enzyme-catalysed reaction reaches a maximum when the substrate concentration is in excess. Here, the reaction is zero-order with respect to the substrate concentration.

Rearranging eq83 to shows that at low initial substrate concentration (), the reaction approximates first-order kinetics for a fixed : .

When , we have .

At a specific temperature and pH, is characteristic for a given enzyme-substrate pair. It can be interpreted as a measure of the affinity of the enzyme for its substrate because it can be rewritten as:

Here,  is the equilibrium constant for . A smaller  (and hence a smaller ) corresponds to greater the affinity of the enzyme for its substrate, since the enzyme–substrate complex is less likely to dissociate back into free enzyme and substrate. Additionally, because is equal to the substrate concentration at which the reaction rate is half-maximal, a smaller means the enzyme can achieve this rate at lower substrate concentrations and therefore operates more efficiently.

 

 

To determine experimentally, is rearranged into a Lineweaver-Burk form:

A plot of against for different initial substrate concentrations results in a straight line with intercept  and slope , from which can be determined (see diagram below).

 

Previous article: Radiocarbon dating

Content page of intermediate chemical kinetics

Content page of intermediate chemistry

Main content page

The pK_a of an amino acid is the specific pH at which one of its ionisable groups is 50% protonated.

This concept is central to understanding how amino acids behave in different chemical and biological environments. Because amino acids contain multiple ionisable groups (typically an amino group, a carboxyl group and sometimes an ionisable side chain), their charge state can change depending on the surrounding pH. This directly affects properties such as solubility, structure, and interactions with other molecules, especially in proteins where even small shifts in charge can alter folding or function.

 

 

Several factors influence the pK_a values of amino acids, including:

• • Resonance stabilisation.
  • Inductive effects.
  • Intramolecular hydrogen bonding.
  • The local environment surrounding the amino acid.

 

Resonance stabilisation

Functional groups that can delocalise electrons in the conjugate base lower pK_a values. In other words, the more stable the conjugate base, the stronger the acid, and thus the lower its pK_a. Carboxyl groups generally have lower pK_a values (more acidic) than amino groups because their negative charge, once deprotonated, is stabilised by resonance. In contrast, amino groups tend to hold onto their protons more strongly, resulting in higher pK_a values.

For example, when the phenolic group of tyrosine loses a proton (pK_a ≈ 10.46), the negative charge is delocalised into the benzene ring and the conjugate base is resonance-stabilised. In comparison, the pK_a of cyclohexanol is about 16 (negative charge of the conjugate base is not delocalised and remains on the oxygen atom).

Resonance stabilisation also applies to the amine group of an amino acid, increasing its pK_a value and making it a strong base. For instance, the conjugate acid of arginine is stabilised (pK_a ≈ 12.48) when its guanidino group is protonated (c.f. lysine pK_a ≈ 10.54).

 

Inductive effects

An electron-withdrawing group stabilises the negative charge formed after deprotonation of a carboxyl group in an amino acid, thereby lowering its pK_a. Conversely, an electron-donating group destabilises the charged form and increases the pK_a.

For example, the carboxyl group of glycine is more acidic (pK_a ≈ 2.35) than acetic acid (pK_a ≈ 4.76) because its conjugate base is stabilised by both inductive and resonance effects. Notably, the amino group, which is protonated under physiological conditions (pH ≈ 7.4), acts as an electron-withdrawing group.

Another example is aspartic acid. Since the –I effect decreases with distance, the -carboxylate group (pK_a ≈ 1.99) is stabilised more strongly than the -carboxylate group (pK_a ≈ 3.90). Parenthetically, aspartic acid residues in proteins are usually negatively charged at physiological pH, contributing to electrostatic interactions such as salt bridges with positively charged amino acids (e.g. lysine or arginine). This helps to stabilise protein structure.

On the other hand, an alkyl side chain exerts a +I effect on other functional groups in an amino acid. For example, the methyl group in alanine acts as an electron-donating group and increases the electron density on the nitrogen atom of the adjacent amino group, making it a slightly stronger base (pK_a ≈ 9.87) than that of glycine (pK_a ≈ 9.78).

 

 

 

Intramolecular hydrogen bonding

Additionally, intramolecular hydrogen bonding can influence pK_a by stabilising the deprotonated state, lowering the pK_a of the carboxyl group. The hydroxyl group in the side chain of serine may form an intramolecular hydrogen bond with the carboxylate oxygen. This also occurs in threonine, whose pK_a (about 2.09) is slightly lower than that of serine (pK_a ≈ 2.19). While the relatively small substituents attached to the -carbon in serine allow the C_a-C_b bond to rotate more freely, the bulky methyl group in threonine reduces steric hindrance by favouring a gauche conformation, in which the hydroxyl group is positioned closer to the carboxyl group, increasing the probability of forming an intramolecular hydrogen bond. This makes threonine slightly more acidic than serine.

 

Previous article: Improved Henderson-Hasselbalch equation

Content page of strong base to weak acid titration curve

Content page of intermediate chemistry

Main content page

Molecular Orbital (MO) theory states that electrons in a molecule occupy orbitals that span the entire molecule rather than being localised between atoms.

The theory was developed by Friedrich Hund, Robert Mulliken, John Slater and John Lennard-Jones, who proposed that when atoms approach each other to form a molecule, their atomic orbitals overlap and combine mathematically to generate new orbitals called molecular orbitals. This process is known as the linear combination of atomic orbitals (LCAO). In this approach, molecular orbitals are constructed by combining the wavefunctions of the contributing atomic orbitals, analogous to the superposition of waves.

Because each atomic orbital (AO) is described by a wavefunction, the MO wavefunction can be expressed as the sum or difference of the AO wavefunctions. For example, the MO wavefunction of H₂ can be written as:

where and  are the 1s AO wavefunctions of the two hydrogen atoms.

Eq10 represents an approximate solution to the time-independent Schrödinger equation for the H₂ molecule. An equally valid solution is

Since each AO can accommodate a maximum of two electrons, the orbital conservation principle of MO theory states that the total number of MOs formed must equal the total number of AOs combined to produce them. Incidentally, the two solutions for H₂ correspond to different types of MOs: the addition of wavefunctions produces a bonding MO, while their subtraction produces an anti-bonding MO.

Bonding MOs are formed when the overlapping wavefunctions of AOs are in-phase, which leads to constructive interference, and hence a build-up of electron density between the bonding nuclei (see above diagram). The positively-charged nuclei are attracted to the region of higher electron density, resulting in a more stable system. Consequently, a bonding MO has a lower energy than the AOs from which it is formed.

Anti-bonding MOs, denoted by an asterisk (*), are due to the overlapping wavefunctions of AOs being significantly out-of-phase, which results in destructive interference, and therefore a node, between the bonding nuclei. The nuclei are attracted to the non-nodal electron densities, away from the internuclear region. This causes a destabilisation of the system (if the MO is occupied) and the anti-bonding MO having a higher energy than the AOs from which it is formed.

Besides bonding and anti-bonding MOs, a third type, called a non-bonding MO, can appear in molecules that have lone pairs of electrons. For example, in the hydroxyl radical ⋅OH, the hydrogen 1s AO overlaps with the oxygen 2p_z AO to form a bonding MO and an anti-bonding MO, while the oxygen 2p_x and 2p_y AOs, which do not interact significantly with hydrogen due to symmetry, form a pair of degenerate (same energy) non-bonding MOs.

In general, non-bonding MOs are formed when the overlapping wavefunctions of AOs are partially out-of-phase. A non-bonding MO shows neither charge depletion nor charge accumulation between the nuclei. Electrons in such an MO neither contribute to nor reduce bond strength. Therefore, it has approximately the same energy as the AOs from which it is formed.

The relative energies of MOs and the AOs that form them are illustrated using molecular orbital diagrams. These diagrams typically consist of three columns of orbitals (see diagram below). The middle column contains MOs, while the left and right columns show the valence AOs of the atoms that combine to form the MOs. Horizontal lines represent the energy levels of the orbitals, and dotted lines link the MOs to the AOs used to construct them. Each MO has a characteristic symmetry, such as , or .

Electrons fill molecular orbitals according to the same rules used for atomic orbitals. They follow the Aufbau Principle, filling lower-energy orbitals before higher ones, and obey the Pauli Exclusion Principle, which states that no two electrons in the same orbital can have identical quantum numbers. Furthermore, Hund’s Rule, which states that electrons occupy degenerate orbitals singly before pairing, also applies. In the ground state configuration, the highest occupied molecular orbital (HOMO) of a molecule contains the highest-energy electrons. Electrons in the HOMO are the most likely to be donated in chemical reactions, such as nucleophilic reactions or excitation to higher orbitals. In contrast, the lowest unoccupied molecular orbital (LUMO) is the lowest-energy molecular orbital that is unoccupied by electrons. It is the orbital that accepts electrons during chemical reactions, such as electrophilic attack or electronic excitation. Together, the HOMO and LUMO are known as frontier orbitals.

 

 

MO theory also introduces the concept of bond order, which helps predict the strength and stability of a bond. It is defined as:

where and are the number of electrons in the bonding MO and the anti-bonding MO respectively.

A higher bond order indicates a stronger and more stable bond, whereas a bond order of zero suggests that the molecule is unlikely to exist. Bond orders of 1, 2 and 3 are commonly referred to as single, double and triple bonds respectively. In the above examples, the bond order of H₂ is , while the bond order of ⋅OH is also one. Fractional bond orders usually occur in radicals, ions or molecules with delocalised electrons. For instance, the bond order of the dihydrogen cation H₂⁺ is 0.5. This means that bond is weaker and longer than the bond in H₂.

One advantage of MO theory is that it explains properties that earlier bonding models could not, such as the paramagnetism of oxygen molecules, where unpaired electrons are present in molecular orbitals. The theory also provides a quantum-mechanical explanation for the d-orbital splitting described in the ligand field theory, and sheds light on why many transition metal complexes are coloured. Finally, it is the foundation of band theory, which explains how semiconductors work.

In summary, molecular orbital theory describes chemical bonding by forming molecular orbitals from atomic orbitals, distributing electrons across the entire molecule, and using orbital energies and bond order to explain molecular stability and properties.

 

Previous article: Nuclear spin

Content page of intermediate quantum chemistry

Content page of intermediate chemistry

Main content page

The solubility of calcium fluoride, CaF₂, can be analysed quantitatively using thermodynamic and kinetic principles.

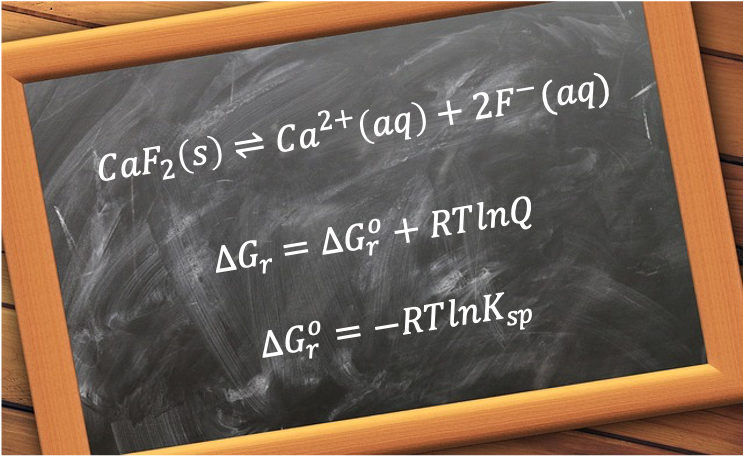
At 25°C, the solubility product of CaF₂ is approximately 3.45 x 10^-11. The equilibrium expression for the reversible reaction is:

Setting and , where is the solubility of CaF₂, yields

 

 

In terms of chemical energetics, CaF₂’s standard enthalpy change of lattice energy, determined using the Born Haber cycle, is +2,635 kJmol^-1, while its total standard enthalpy change of hydration energy is about -2,624 kJmol^-1, resulting in a positive standard enthalpy change of solution of +11.0 kJmol^-1. Because the net enthalpy change is slightly endothermic, the process is not enthalpically favoured. However, the thermodynamic feasibility of a reaction is determined by the change in reaction Gibbs energy:

which includes the factor , and where a negative change in reaction Gibbs energy favours the forward reaction.

To understand why a solution of solid CaF₂ reaches saturation at 2.10 x 10^-4 mol/L, we refer to the expression (see this article for derivation):

where

• • is the change in reaction Gibbs energy under non-standard conditions.
  • is the change in reaction Gibbs energy under standard conditions (pure solids in their standard state, solutes at 1.0 M and T = 298.15 K)
  • is the reaction quotient ( is the activity of species and is the stoichiometric coefficient of species in the reaction). In dilute solutions, the activity of a species is approximately equal to the concentration of the species. At equilibrium, .

At the start of dissolution, very little product is formed (), so and therefore . Hence, some solid CaF₂ must dissolve spontaneously. As the ion concentrations increase and the solubility reaches 2.10 x 10^-4 mol/L, the system attains equilibrium, where . Here, because a reversible reaction at equilibrium is spontaneous in neither direction. Thus, eq21 becomes:

which at 25°C returns the value kJ/mol.

This positive value indicates that forming Ca²⁺(aq) and F⁻(aq), each at 1.0 mol dm⁻³, from solid CaF₂ under standard conditions is not spontaneous. Nevertheless, dissolution initially occurs to a limited extent until equilibrium is established, consistent with its very small solubility product.

 

 

 

Previous article: Reaction Gibbs energy

Content page of chemical thermodynamics

Content page of intermediate chemistry

Main content page

A semiconductor is a crystalline material whose atomic bonding produces a band gap small enough to allow controllable charge-carrier generation and conductivity between that of a conductor and an insulator.

Silicon (Si) and gallium arsenide (GaAs) are common base materials in the manufacture of semiconductors. Si has a diamond cubic crystal structure, where each Si atom, which has four valence electrons, is covalently bonded to four neighbouring Si atoms, forming a tetrahedral arrangement. When boron (B), a trivalent element, is added, it replaces a Si atom in the lattice. Since B has only three valence electrons, it forms three covalent bonds with neighbouring Si atoms, leaving one bond unfulfilled. This unfulfilled bond, which lacks an electron, is known as a “hole”. With sufficient energy, such as in the presence of an electric field, an electron from a neighboring Si atom can move into the hole, forming a covalent bond with the B atom (the acceptor atom) and leaving a new hole in its original position. The ionised B atom becomes negatively charged, while the ionised Si atom is positively charged. As this process repeats, the hole (or the positively charged atom) appears to move through the lattice in the opposite direction to the movement of the electrons. This type of doped material is called a p-type semiconductor (see diagram below).

The above phenomenon can also be understood through molecular orbital (MO) theory. When two atoms overlap, two MOs are formed: a bonding orbital and an antibonding orbital. For three atoms, three MOs are produced — bonding, non-bonding and antibonding — while the orbital overlap of four atoms results in four MOs: two bonding and two antibonding orbitals. In general, a chain of atoms generates molecular orbitals. If is large, the energy levels of these MOs merge to form an energy band (see diagram below).

At the ground state of solid Si, the highest energy band that is filled with electrons is known as the valence band. The next higher energy band, the conduction band, can be filled if sufficient energy excites electrons in the valence band to move into it. The energy difference between the valence band and the conduction band is called the band gap, the magnitude of which depends on the type of base material used.

Conversely, when phosphorus (P), a pentavalent element, is introduced, it forms four covalent bonds with neighbouring silicon atoms using four of its valence electrons. The fifth electron, however, is not involved in bonding and remains loosely bound to the P atom. This electron can be easily excited to the conduction band with a small amount of thermal energy, allowing it to move freely through the lattice and leaving the ionised donor P atom positively charged. As a result, the addition of P creates an n-type semiconductor (see diagram below), where free electrons contribute to electrical conductivity.

Another base semiconductor material is gallium arsenide (GaAs), where each gallium (Ga) atom is tetrahedrally coordinated to four arsenic (As) atoms, and vice versa, resulting in no free electrons available to conduct electricity. If an impurity like beryllium is added to GaAs, it replaces a Ga atom and introduces holes (p-type) into the material because Be has only two valence electrons. On the other hand, when Si is used as a dopant, it substitutes for Ga, resulting in an n-type semiconductor.

The magic happens when a p-type semiconductor is connected to an n-type semiconductor, creating a p-n junction (see diagram below). Free electrons (negative charge carriers) from the n-type side begin to diffuse into the p-type side, where they recombine with holes. This recombination reduces the number of free carriers on the p-type side near the junction, leaving behind positively charged donor ions on the n-type side. Similarly, holes (positive charge carriers) from the p-type side diffuse into the n-type side and recombine with free electrons, leaving behind negatively charged acceptor ions in the p-type side. This process establishes an electric field across the junction that opposes further diffusion of carriers. Eventually, a state of equilibrium is reached where the diffusion of electrons and holes is balanced by the electric field, generating a depletion region — an electrically neutral region devoid of any mobile charge carriers. This equilibrium can be easily disrupted when electrons from the n-type side gain additional energy from an external source.

When a voltage is applied across the p-n junction, with the positive terminal connected to the p-type material and the negative terminal connected to the n-type material, forward bias occurs (see diagram below). In this state, electrons from the n-type material gain energy and cross the junction into the p-type material. The majority recombine with holes, while a small fraction continues to drift through the p-type material and into the external circuit, contributing to the current flowing through the device.

In the MO model, electrons flowing in the circuit are in the conduction band. Some of them relax to a more stable state in the valence band during recombination of a free electron with a hole. When this occurs, a photon with energy corresponding to the semiconductor’s band gap energy is emitted. Such a circuit design is known as a light-emitting diode (LED), with the colour of the emitted light determined by the band gap energy. For instance:

• • Infrared LEDs (e.g. GaAs) emit light at longer wavelengths, around 850 nm.
  • Red LEDs (e.g. GaAlAs) emit at approximately 630 nm.
  • Green LEDs (e.g. InGaN) emit around 525 nm.
  • Blue LEDs (e.g. InGaN) emit at about 470 nm.

But why is it called a diode?

If a reverse voltage is applied, it increases the electric field across the p-n junction. This results in more electrons being pulled away from the junction in the n-type region and more holes being pulled away from the junction in the p-type region, leading to the widening of the depletion region. This ultimately prevents the movement of the charge carriers when a steady-state is attained, a condition we refer to as reverse bias.

Consequently, a p-n junction functions as a diode, which is a device that allows current to flow in one direction while blocking it in the reverse direction (see diagram below). A regular diode, one that does not emit light when current passing through it, has moderately doped p and n regions, while an LED generally has heavily doped p and n regions. This higher doping concentration increases the probability of electron-hole recombination, which is essential for light emission.

By adjusting the intensities of red, green and blue (RGB) LEDs, the three different coloured LEDs can be combined to create a wide range of white light shades. These “white” LEDs are widely used in home lighting, automotive lighting and electronic displays.

 

Previous article: Covalent and molecular solids

Content page of solids

Content page of intermediate chemistry

Main content page

 

Radioactive decay is the spontaneous process by which an unstable atomic nucleus transforms into a more stable one by emitting particles or energy.

It follows first-order kinetics, meaning the rate at which a radioactive nucleus transforms is directly proportional to the number of un-decayed nuclei  at any given time . Because each nucleus decays independently, the probability that a nucleus will decay in a small interval of time is constant, regardless of how long the atom has existed. Mathematically, the rate law is given by:

where is dimensionless, and , the decay constant, represents the probability of decay per unit time.

An example of radioactive decay is the transformation of uranium-238 into thorium-234 with the emission of an alpha particle (a helium nucleus):

Thorium-234, which is also radioactive, then undergoes beta decay (a beta particle is an electron) to produce protactinium-234, and continues through a chain until a stable lead-206 nucleus is formed:

 

 

Solving eq60 by integration gives:

where is the number of un-decayed nuclei at .

Therefore, the probabilistic decay behaviour leads to an exponential decrease in the number of radioactive nuclei as time passes.

For a first order reaction, the half life is constant and given by:

Because is specific to each radioactive isotope, every radionuclide has a characteristic half-life, which can be exploited to gain insight into the age of a material. For example, the analysis of radioactive elements within meteorites allow scientists to estimate the age of the earth. One commonly used method involves the decay of uranium-238 to lead-206. Uranium-238 has a half-life of about 4.47 billion years, meaning that after this time, half of the original ²³⁸U atoms in a sample will have decayed to ²⁰⁶Pb. By measuring the present-day ratio of parent isotope (²³⁸U) to daughter isotope (²⁰⁶Pb) in ancient minerals, such as zircon crystals found in some of the oldest meteorites, scientists can determine how many half-lives have elapsed.

 

 

Suppose zircon samples from the oldest meteorite on Earth are measured by TIMS to have values very close to:

From eq61, the number of ²³⁸U atoms remaining at time is:

Zircon (ZrSiO₄), during its initial formation, incorporates U⁴⁺ easily but not Pb²⁺ because U⁴⁺ closely matches Zr⁴⁺ in both charge and ionic radius, allowing it to substitute easily, whereas Pb²⁺ has a lower charge and a much larger radius, making substitution energetically unfavourable. Therefore, lead is typically below detection levels initially, and the number of ²⁰⁶Pb atoms formed is:

It follows that the uranium-to-lead ratio can be expressed as:

Solving for yields:

Substituting eq62, where billion years, into eq64 gives billion years. Since represents the time required for the original ²³⁸U to produce the measured uranium-to-lead ratio of 0.99, the earth is therefore approximately 4.5 billion years old.

 

 

NExt article: Radiocarbon dating

Previous article: Iodine clock experiment

Content page of intermediate chemical kinetics

Content page of intermediate chemistry

Main content page

Radiocarbon dating is a method of determining the age of carbonaceous materials by measuring the amount of radioactive carbon-14 remaining in them.

Developed by the chemist Willard F. Libby (see above picture) in 1949, radiocarbon dating, also known as carbon-14 dating, is one of the most widely used techniques in archaeology, paleontology and environmental science because it allows scientists to estimate when an organism died. The method is based on the radioactive decay of ¹⁴C, an unstable isotope of carbon that forms naturally in the upper atmosphere.

When cosmic rays strike atmospheric ¹⁴N, a small but fairly constant amount of ¹⁴C is produced:

This radioactive carbon combines with oxygen to form carbon dioxide, which plants absorb through photosynthesis. Animals then consume the plants and incorporate ¹⁴C into their bodies. As long as an organism is alive, it constantly exchanges carbon with the environment, keeping the ratio of stable ¹²C to radioactive ¹⁴C roughly constant.

When an organism dies, however, it stops taking in carbon. From that moment on, the ¹⁴C in its tissues begins to decay at a known rate, transforming back into ¹⁴N through beta decay:

The decay rate is characterised by ¹⁴C’s half-life of 5,730 years. By comparing the amount of ¹⁴C remaining in a dead organism to the amount it would have contained while alive, scientists can determine how long it has been since the organism died.

The fundamental principle behind the method is expressed mathematically using the first-order radioactive decay equation:

where

is the amount of radioactive carbon remaining after time .
is the original amount at the time of death.
is the decay constant, and is related to the half-life of the decaying species by .
is the time that has passed since death.

To illustrate how radiocarbon dating calculations work, consider the example of an archaeological team that discovers a wooden tool handle at an ancient settlement. The ratios of ¹⁴C to ¹²C in a sample of the tool and in modern wood of the same type are analysed using mass spectrometry to be and respectively.

Because all living organisms share essentially the same carbon isotopic composition as the contemporary atmosphere, any decrease in ¹⁴C relative to ¹²C reflects radioactive decay occurring after death. Assuming that the concentration of the stable isotope ¹²C is the same in the sample and in modern wood, the fraction of radiocarbon remaining in the sample is:

Combining the radioactive decay equation with the half-life equation gives:

Substituting eq70 and ¹⁴C’s half-life of 5,730 years into eq71 yields years, which is the uncalibrated radiocarbon age of the wooden tool.

Although the raw radiocarbon age can be calculated precisely, it does not necessarily correspond directly to calendar years. The amount of ¹⁴C in the atmosphere has not been constant over time; it has fluctuated with solar activity, geomagnetic field strength, ocean circulation changes, and most recently human activities such as fossil fuel burning and atmospheric nuclear tests. To correct for these variations, radiocarbon ages must be calibrated using independent chronological records, most importantly tree-ring sequences (dendrochronology). Calibration curves allow raw radiocarbon ages to be converted into more accurate calendar ages.

Finally, radiocarbon dating is reliable for materials up to about 50,000–60,000 years old. Beyond that point, so little ¹⁴C remains that it becomes difficult to distinguish from background radiation and measurement noise. Despite these complications, radiocarbon dating remains extraordinarily valuable. It has been used to date archaeological sites, reconstruct past climates, verify the authenticity of historical artifacts, and study ecological changes. For instance, it helped determine the age of the Dead Sea Scrolls, revealed the timing of glacial advances and retreats, and allowed scientists to track how ancient cultures expanded or declined.

 

Next article: Michaelis-Menten equation

Previous article: Radioactive decay

Content page of intermediate chemical kinetics

Content page of intermediate chemistry

Main content page

The Clausius-Clapeyron equation describes how the vapour pressure of a pure substance changes with temperature during a phase change. It has the form

where

is the vapour pressure,
is the enthalpy of vaporisation or enthalpy of sublimation,
is the universal gas constant,
is the temperature in Kelvin,

We can derive the Clausius-Clapeyron equation from the van’t Hoff equation , where for phase transitions such as or , the activity of the pure liquid or solid phase in the equilibrium constant is taken as 1. This simplifies the expression and leads to eq 26.

 

Previous article: Effect of catalysts on equilibria

Content page of chemical equilibrium

Content page of intermediate chemistry

Main content page