Category: Intermediate Chemistry

Posted on

How to prepare a buffer solution?

How do we prepare a buffer solution?

In the previous article, we explained the factors affecting the buffer capacity of a solution. To prepare an effective buffer (e.g. an acidic buffer), we need to:

      1. Select a weak acid with a pKa  value at a specific temperature that closely matches the desired pH for the buffer at that temperature.
      2. Choose a corresponding conjugate base, i.e. salt of the weak acid.
      3. Use the Henderson-Hasselbalch equation to calculate the ratio of the conjugate base concentration to the weak acid concentration, which should be as close to unity as possible to achieve maximum buffer capacity.
      4. Calculate the volumes and concentrations of the weak acid and its conjugate base for mixing.

 

Question

How to prepare 500.0 ml of a buffer to maintain a pH of 4.6?

Answer

Step 1: Use 1.0 M acetic acid (\(pK_a=4.757\))

Step 2: Choose sodium acetate (Ar = 82.03)

Step 3: Substitute values in the Henderson-Hasselbalch equation

4.6=4.757+log\frac{[CH_3COO^-]}{[CH_3COOH]}\; \; \; \; \; \Rightarrow \; \; \; \; \;\frac{[CH_3COO^-]}{[CH_3COOH]}=0.697

Step 4: Since [CH3COOH] = 1.0,  [CH3COO–] = 0.697 M

The mass of solid sodium acetate m needed to dissolve in 500.0 ml of 1.0 M acetic acid to achieve a concentration of 0.679 M is:

\frac{m}{82.03}/0.5=0.697\; \; \; \; \; \Rightarrow \; \; \; \; \; m=28.6\: g

 

Next article: Effect of dilution on the pH of a buffer
Previous article: Factors affecting buffer capacity
Content page of introduction to buffer solutions
Content page of intermediate chemistry
Main content page
Posted on

Factors affecting buffer capacity

What are the factors affecting the capacity of a buffer solution?

The effectiveness (or capacity) of a buffer is dependent on a few factors, namely,

    1. Absolute concentrations of the conjugate acid and conjugate base.
    2. Relative concentrations of the conjugate acid and conjugate base.
    3. pKa (for an acidic buffer) of the weak acid in relation to the pH that the buffer is intended to maintain.
    4. Absolute value of pKa.
    5. Temperature.

To rationalise the first factor affecting buffer capacity, we refer to the acidic buffer equilibrium:

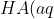HA(aq)+H_2O(l)\rightleftharpoons A^-(aq)+H_3O^+(aq)

As mentioned in the previous article, a base OH– added to the buffer reacts with H3O+ to form water. According to Le Chatelier’s principle, the system counteracts this change by shifting the above equilibrium to the right, with some HA further dissociating to replace the H3O+ that has been removed. The higher the concentration of the conjugate acid HA, the greater the amount of HA that can replace the removed H3O+. Similarly, the larger the amount of the conjugate base A–, the greater the buffer’s ability to react with any acid that is added. Hence, buffer capacity is proportional to the combined concentrations of the conjugate acid and conjugate base. Mathematically, the buffer capacity of a weak conjugate acid/conjugate base pair is given by the following equation (see this article for derivation):

\beta_a=\frac{[HA]_TK_a[H^+]ln10}{\left ( K_a+[H^+] \right )^2}

where [HA]T = [HA] + [A–], i.e. the analytical concentration of HA.

The equation clearly shows that the buffer capacity of an acidic buffer is proportional to the combined concentrations of the conjugate acid and conjugate base.

The second factor states that the relative concentrations of the conjugate acid and conjugate base affects buffer capacity. In fact, the maximum buffer capacity of a solution occurs when the concentration of the conjugate acid equals to the concentration of the conjugate base (see this article for details). Substituting \frac{[A^-]}{[HA]}=1 into the Henderson-Hasselbalch equation, we have pH = pKa. In other words, for an acidic buffer to achieve maximum buffer capacity, the pKa of the chosen weak acid must be as close as possible to the pH that the buffer is intended to maintain. This is how the third factor affects buffer capacity.

It is also important to select an acid with pKa that is neither too high nor too low (fourth factor). An acid with a pKa < 3 (Ka > 10-3) is a relatively strong acid with a high degree of dissociation. Likewise, an acid with a pKa > 11 (Ka < 10-11) is a relatively strong base. As explained in this article, a strong acid (or a strong base) has very low or negligible buffer capacity.

Finally, the buffer capacity of a solution is affected by changes in temperature (fifth factor) since the equilibrium constant is temperature-dependent:

lnK=-\frac{\Delta _rG^o}{RT}

This implies that pKa is also temperature-dependent.

In short, these five factors are important in preparing a buffer solution, which we will discuss in the next article.

Next article: How to prepare a buffer solution?
Previous article: Overview
Content page of introduction to buffer solutions
Content page of intermediate chemistry
Main content page
Posted on

Introduction to buffer solutions: overview

A buffer solution is one that resists changes in pH upon dilution or the addition of acids and bases. The pH of a buffer solution does change when diluted or when acids and bases are added but the change is much less than that compared to an unbuffered solution.

A buffer solution is usually composed of a weak conjugate acid-base pair, e.g. the ethanoic acid/ethanoate pair (acidic buffer) or the ammonium chloride/ammonia pair (basic buffer). It is most effective (or has a maximum buffer capacity) when it contains equal equilibrium concentrations of the weak acid and its conjugate base.

For an acidic buffer, we have the following equilibrium:

HA(aq)+H_2O(l)\rightleftharpoons A^-(aq)+H_3O^+(aq)

If a small amount of acid H3O+ is added to the solution, it reacts with the conjugate base A– to form the weak conjugate acid HA, thereby removing the added acid and resisting the change in pH. Similarly, when a small amount of base OH– is added, it combines with H3O+ to form water; again, resisting the change in pH. The degree to which a buffer solution resists the change in pH is dependent on a few factors, which shall be discussed in the next article.

 

Next article: Factors affecting buffer capacity
Content page of introduction to buffer solutions
Content page of intermediate chemistry
Main content page
Posted on

Improved Henderson-Hasselbalch equation

The improved Henderson-Hasselbalch equation, a modified version of the original formula, provides a better approximation of the shape of a titration curve than the original equation.

In deriving the Henderson-Hasselbalch equation, we made the following three assumptions:

    • [H+] from water is negligible, i.e. H+ in the flask containing the weak acid is solely due to that of the acid, [H+]a as the dissociation of water is again suppressed at this stage.
    • For a weak acid, [HA] is approximately equal to the concentration of the undissociated acid, [HA]ud, i.e. the dissociation of the weak acid HA is negligible and the remaining concentration of HA after the addition of base is [HA]r = [HA]ud – [A–]s.
    • [A–] is approximately equal to the concentration of the salt, [A–]s, in the solution, i.e. A– is completely attributed to the salt formed, with no contribution from the further dissociation of HA.

However, the Henderson-Hasselbalch equation is unreliable when Ka ≥ 10-3. If we disregard the 2nd and 3rd assumptions, the equilibrium expression is:

K_a=\frac{[H^+]_a\left ( [A^-]+[H^+]_a \right )}{[HA]-[H^+]_a}

Rearranging the above equation and solving the quadratic equation in [H+]a,

[H^+]_a=\frac{-\left ( [A^-]+K_a \right )+\sqrt{\left ( [A^-]+K_a \right )^2+4K_a[HA]}}{2}

pH=-log\frac{-\left ( [A^-]+K_a \right )+\sqrt{\left ( [A^-]+K_a \right )^2+4K_a[HA]}}{2}

pH=-log\frac{-\left ( \frac{C_bV_b}{V_a+V_b}+K_a \right )+\sqrt{\left ( \frac{C_bV_b}{V_a+V_b}+K_a \right )^2+4K_a\frac{C_aV_a-C_bV_b}{V_a+V_b}}}{2}\; \; \; \; \; \; \; \; (6)

where Ca and Cb are the analytical concentrations of the acid and base respectively (i.e. the concentrations of the acid and base before any dissociation occurs). Eq6 is the improved version of the Henderson-Hasselbalch equation.

The diagram below shows the superimposition of eq6 (green curve) over the complete pH titration curve (red curve) that disregard all three assumptions, for the titration of 10 cm3 of 0.200 M of CH3COOH (Ka = 1.75 x 10-5) with 0.100 M of NaOH.

The fit is much better than the Henderson-Hasselbalch curve even though the two curves (i.e. eq6 and the complete pH titration curve) do not actually coalesce and are still two separate curves when the axes of the plot are scaled to a very high resolution. Furthermore, eq6 doesn’t become invalid when Ka ≥ 10-3, for example, the diagram below is the superimposition of eq6 on the complete pH titration curve for the titration of 10 cm3 of 0.200 M of an acid (Ka = 1.75 x 10-2) with 0.100 M of NaOH:

If we further superimpose the Henderson-Hasselbalch curve (purple curve) onto the above diagram for the same titration, we have,

Clearly, the Henderson-Hasselbalch equation breaks down when Ka ≥ 10-3.

 

Previous article: Combining all equations
Content page of strong base to weak acid titration curve
Content page of intermediate chemistry
Main content page
Posted on

Mass spectrometry application: structure elucidation

Mass spectrometry is used to identify structures of organic compounds. The sample to be analysed is vaporised, fed into the ioniser and fragmented by bombarding electrons. By using knowledge of the relative masses and abundances of isotopes that make up the compound, or by referencing the spectra of known substances, the structure of the compound can be determined. For example,

Question

With reference to the spectrum below, deduce the structure of an organic compound that forms a sweet smelling liquid with acetyl chloride.

Answer

The sweet smelling liquid could be an ester and hence the organic compound could possibly be an alcohol. Assuming that it is a simple alcohol, its general formula is CnH2n+1OH.

Look for the peak representing the molecular ion (M+), i.e. the unfragmented sample molecule with one electron removed. This peak should have one of the highest u/z values and a relatively high abundance.

The highest peak is at 33 u/z but has a negligible abundance. Hence, the peak at 32 u/z is most probably the molecular ion. If so,

M_r\left ( C_nH_{2n+1}OH \right )=32

12n+2n+1+16+1=32

n=1

Hence, the organic compound could be methanol, CH3OH. We can verify our guess by analysing the other peaks:

u/z

 Molecule Formula

Logic

33

 M++1 13CH3OH

13C has an abundance of only 1.07%, but much higher than that of 17O, 18O and 2H.

32

 M+ 12CH3OH

One of the highest u/z and high abundance

31

 M+-1 12CH3O+

Cleavage of polarised O-H bond; relatively stable and thus high abundance

30

 M+-2 12CH2O+

Loss of 1 proton attached to C and one to O

29

 M+-3 12CHO+

Loss of 2 protons attached to C and one to O

28

 M+-4 12CO+

Full deprotonation

15

 M+-7 12CH3+

Cleavage of polarised -OH bond

With the above deductions, we can conclude that the spectrum is one for methanol.

 

 

next article: Other forms of mass spectrometry
Previous article: Applcation: relative atomic mass
Content page of mass spectrometry
Content page of intermediate chemistry
Main content page
Posted on

Other forms of mass spectrometry

Mass spectrometers can be combined with other instruments to form powerful analytical tools. One such example is the Gas Chromatography-Mass Spectrometer (GC-MS), which combines a gas chromatograph with a mass spectrometer (see diagram below).

The concept of gas chromatography is similar to that of paper chromatography except that both the sample and the mobile phase are gases rather than liquids. In GC-MS analysis, the sample first passes through the gas chromatograph, where different types of molecules are retained by the stationary phase for varying durations before flowing into the mass spectrometer. There, the molecules are fragmented and analysed.

The resulting data are presented on a three dimensional graph with retention time, mass-to-charge ratio and relative abundance as the axes. Consequently, a GC-MS spectrum contains more information about the sample than a TIMS spectrum. GC-MS is commonly used by border security forces to detect narcotics and explosives in luggage or on individuals, as well as by environmental agencies to monitor airborne pollutants.

Another important instrument is the Inductively Coupled Plasma Mass Spectrometer (ICP-MS), which is capable of detecting trace amounts of metals and non-metals (see diagram below). The main difference between an ICP-MS and a TIMS is the use of an inductively coupled plasma (a concentration of argon ions and electrons that is produced by inductively heating argon with an electromagnetic coil) to ionise the sample. ICP-MS has greater speed, precision, and sensitivity over TIMS and is used in the fields of medicine, toxicology, forensics, radiometric dating, pharmacy, etc.

Previous article: Application: structure elucidation
Content page of mass spectrometry
Content page of intermediate chemistry
Main content page
Posted on

Mass spectrometry application: relative atomic mass

Mass spectrometry plays a crucial role in determining relative atomic mass by accurately measuring the masses of isotopes in a sample, providing essential data for understanding elemental abundance and chemical properties.

As mention in an earlier article, the relative masses of isotopes can be determined by comparing the charge-to-mass ratio of an isotope of interest with that of carbon-12. For example, mass spectrometric data for the ratio of the mass-to-charge ratio (u/z) of 2H to that of 12C is 0.167842. Thus, the relative mass of 2H on the carbon-12 unified atomic mass unit scale is:

u\; of \; ^{2}H=\frac{u/z\; of\;\; ^2H}{u/z\; of\; \; ^{12}C}\; \times \; u\; of\; ^{12}C

u\; of \; ^{2}H=0.167842\times 12\, u

u\; of \; ^{2}H=2.014104\, u

Consequently, the relative atomic mass of an element can be calculated from its isotopic abundance spectrum.

With reference to the spectrum above, the relative atomic mass of chlorine is:

A_{r,Cl}=\frac{100\times 34.969}{100+31.96}+\frac{31.96\times 36.966}{100+31.96}=35.45

Question

Deduce the spectrum for the chlorine gas ion, Cl2+.

Isotope

 Relative isotopic mass

Relative abundance, %

35Cl

 35

75.78

37Cl

 37

24.22
Answer

Assuming a random distribution of isotopes in the sample of chlorine gas and no fragmentation, the possible permutations of chlorine isotopes in a chlorine gas ion are:

Permutation, XClYCl+

 Relative isotopic mass

No. of permutations

35Cl35Cl

 70

1

35Cl37Cl or 37Cl35Cl

 72

2

37Cl37Cl

 74

1

The probability of observing each permutation is:

Permutation, XClYCl+

Probability = abundance X x abundance Y x no. of permutations

35Cl35Cl

0.7578 x 0.7578 x 1 = 0.5742

35Cl37Cl or 37Cl35Cl

0.7578 x 0.2422 x 2 = 0.3671

37Cl37Cl

0.2422 x 0.2422 x 1 = 0.0587

Hence, the spectrum has the following characteristics:

Permutation

 Relative isotopic mass Relative abundance (%)

% of predominant peak

35Cl35Cl

 70 57.42

100.00

35Cl37Cl or 37Cl35Cl

 72 36.71

63.93

37Cl37Cl

 74 5.87

10.22

The values for ‘% of predominant peak’ are calculated relative to the abundance of 35Cl35Cl.

 

Here’s another way to explain the permutation of isotopes in chlorine gas:

Chlorine gas is formed by the collision of two chlorine atoms. Consider an infinitesimal two-dimensional space in a vessel that is filled with chlorine atoms, with the space large enough to accommodate two chlorine atoms (see diagram below).

If we further consider a single axis of collision through that space, and that chlorine atoms are approaching the space along that axis from the left and from the right, we end up with four possible products: 35Cl35Cl, 35Cl37Cl, 37Cl35Cl and 37Cl37Cl. If the abundances of 35Cl and 37Cl are equal, we have twice as many chlorine molecules with mixed isotopes than 35Cl35Cl or 37Cl37Cl, i.e. in the ratio of 2:1:1. If the abundances of 35Cl and 37Cl are unequal, we multiply the numbers in the ratio with the respective abundances of isotopes to get the probabilities of occurrence of the three molecular species. The same result is obtained if we rotate the axis of collision in any direction in three dimensions, or if the collision happens at an angle.

 

next article: application: structure elucidation
Previous article: Modern mass spectrometer design
Content page of mass spectrometry
Content page of intermediate chemistry
Main content page
Posted on

Modern mass spectrometer design

The modern mass spectrometer, an advanced analytical instrument, precisely measures the mass-to-charge ratios of ions, enabling detailed analysis of molecular composition and structure across a wide range of scientific fields.

As mentioned in an earlier article, J. J. Thomson constructed one of the earliest mass spectrometers and conducted the well-known experiment to determine the mass-to-charge ratio of an electron. Since then, different mass spectrometer designs have been developed. For instance, a typical modern Thermal Ionisation Mass Spectrometer (TIMS) consists of the following:

    • Ioniser, where the sample to be analysed is bombarded by electrons to form ions and ion fragments, which are then accelerated into the mass analyser.
    • Mass analyser that utilises a magnetic field to deflect and separate the ions according to their mass-to-charge ratios (u/z). Note that the mass-to-charge ratios before the 1980s were quoted in u/e where e is the charge of an electron instead the number of charges, which is z.
    • Detector that measures the abundance of ions with reference to their mass-to-charge ratios and converts the data into electrical signals.

The result is a plot of ion abundance versus mass-to-charge ratio, with the height of the peaks normalised to the most abundant ion in the spectrum.

 

next article: application: relative atomic mass
Previous article: application: relative isotopic mass
Content page of mass spectrometry
Content page of intermediate chemistry
Main content page
Posted on

How to select an appropriate pH indicator for titration?

How do we select an appropriate pH indicator for titration?

Let’s consider the same indicator as in the previous article: bromocresol green. If the pH of the analyte containing bromocresol green is between 0 and 3.8, it appears yellow; if the pH is between 5.4 and 14, it appears blue. Between 3.8 and 5.4, the colour changes from yellow to blue as the concentration ratio of [In–]/[HIn] changes from 10 to 0.1. In fact, when [In–] = [HIn], the colour of the titrand is green, indicating equal amounts of the yellow acid and the blue conjugate base.

Therefore, bromocresol green is a suitable indicator for a titration with a stoichiometric point (SP) that involves a sharp change of pH from less than 3.8 to more than 5.4 when about 0.1 cm3 of solution (about two drops) is added to the analyte. For example, the titration of 10 cm3 of 0.200 M of HCl with 0.100 M of NaOH sees a colour change of yellow to blue at the SP (see table and graph below).

One drop before SP

SP

One drop after SP

Volume, cm3

19.95

20.00

20.05

pH

3.78

7.00

10.22

In other words, a suitable pH indicator for titration is one whose pH range is narrower than and within the range of the change in pH of the analyte at the stoichiometric point (ideally with one or two drops of solution added).

Another example is the titration of 10 cm3 of 0.200 M of aqueous NH3 (Ka = 1.8 x 10-5) with 0.100 M of HCl, which sees a colour change from blue to yellow at the SP (see table and graph below).

One drop before SP

SP

One drop after SP

Volume, cm3

19.95

20.00

20.05

pH

6.65

5.22

3.78

The following table lists some common indicators and their pH ranges:

Indicator

 Low pH colour pH range High pH colour

pKa

Thymol blue (first transition)

 red 1.2 – 2.8 yellow

1.65

Thymol blue (second transition)

 yellow 8.0 – 9.6 blue

8.96

Methyl yellow

 red 2.9 – 4.0 yellow

3.30

Bromophenol blue

 yellow 3.0 – 4.6 blue 3.85
Congo red blue-violet 3.0 – 5.0 red

4.10

Methyl orange

 red 3.1 – 4.4 yellow 3.46

Screened methyl orange (second transition)

 purple-grey 3.2 – 4.2 green 3.70

Bromocresol green

 yellow 3.8 – 5.4 blue 4.66

Methyl red

 red 4.4 – 6.2 yellow

5.00

Bromothymol blue (second transition)

 yellow 6.0 – 7.6 blue

7.10
Phenol red yellow 6.4 – 8.0 red

7.81

Phenolphthalein (second transition)

 colorless 8.3 – 10.0 purple-pink 9.30
Thymolphthalein (second transition) colorless 9.3 – 10.5 blue

9.90

Alizarine Yellow R

 yellow 10.2 – 12.0 red 11.2
Indigo carmine blue 11.4 – 13.0 yellow

12.2

 

Next article: structures of common indicators
PREVIOUS ARTICLE: THE PH RANGE OF AN INDICATOR
Content page of ph indicators
Content page of Intermediate chemistry
Main content page
Posted on

Structures of common indicators

The diverse chemical structures of common pH indicators, ranging from simple organic dyes to complex conjugated systems, play a crucial role in their ability to visually signal changes in acidity and alkalinity.

Methyl orange is a commonly used indicator. At low pH, protonation of the nitrogen at the para position of the benzenesulphonate moiety is preferred over protonation of the negatively charged oxygen in the sulphonate group, as this confers resonance stabilization (benzenoid-quinonoid tautomerism) to the acid form of methyl orange.

Litmus, extracted from lichen, is processed and applied onto filter paper. It has a pH range of 4.5 to 8.3 and contains the chromophore, 7-hydroxyphenoxazone, which occurs in the following states:

Phenolphthalein has three pKa values with four different forms. However, stoichiometric points of titrations are most commonly monitored with the middle pKa value of 9.30, which involves the lactone and phenolate (dianionic) forms:

Thymol blue has two transition range with pKa1 = 1.65 and pKa2 = 8.96.

Diphenylamine acts as a redox indicator in titrations involving potassium dichromate (K₂Cr₂O₇). In a typical redox titration (e.g. FeSO4 with K₂Cr₂O₇), once all Fe²⁺ is converted to Fe3⁺, any excess dichromate will begin to oxidise diphenylamine, which changes colour — typically from colourless to a deep blue or violet, indicating that the endpoint has been reached.

Previous article: How to select an appropriate ph indicator for titration?
Content page of ph indicators
Content page of Intermediate chemistry
Main content page
Mono Quiz