Category: Intermediate Chemistry

Posted on

Kinetic theory of gases (overview)

The kinetic theory of gases describes the macroscopic properties of gases by analysing gaseous behaviour at the molecular level.

The theory assumes that a gas is composed of point masses moving randomly with different velocities in straight lines within a container. As they move, they may collide elastically with each other or with the walls of the container. The first important concept of the kinetic theory of gases is the root mean square speed of a gas.

 

Next article: Standard deviation
Content page of kinetic theory of gases
Content page of intermediate chemistry
Main content page
Posted on

Spin-spin coupling (nuclear-magnetic resonance)

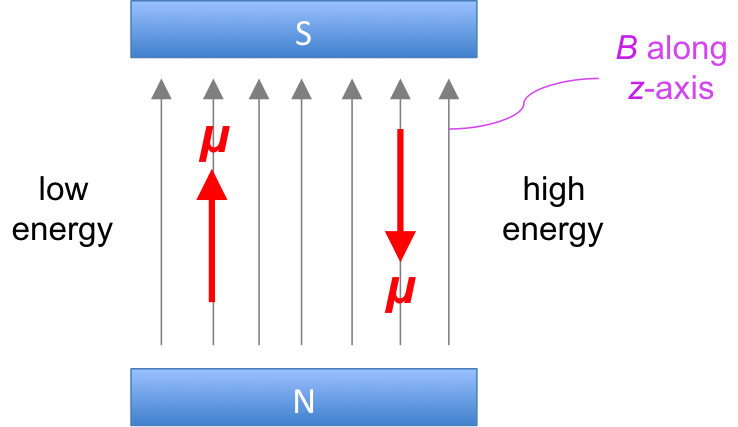
Spin-spin coupling in nuclear magnetic resonance spectroscopy refers to the magnetic interactions between neighbouring nuclei that are not equivalent, leading to a change in resonance frequencies of the nuclei. As mentioned in an earlier article, the nucleus of an atom possesses a magnetic moment that generates a small magnetic field. If two NMR-active atoms (I ≠ 0) are in vicinity of each other, e.g. protons in the moiety HC-CH, the magnetic field of one 1H can shield or deshield the magnetic field of the other 1H, thereby slightly changing its shielding constant and therefore changing its resonance frequency.

In general, we refer to the following rules to determine the extent of nuclear spin-spin coupling:

    1. Spin-spin coupling occurs in all NMR-active nuclei. However, the coupling between two or more equivalent nuclei results in the same resonance energy of transition and therefore has no effect on the chemical shifts of the nuclei.
    2. Spin-spin coupling is negligible between nuclei separated by four or more bonds, e.g. the protons in HC-CH are separated by 3 bonds and consequently display coupling effects.
    3. The changes in chemical shifts of spin-coupled nuclei are usually much smaller than the difference in chemical shifts between the nuclei.

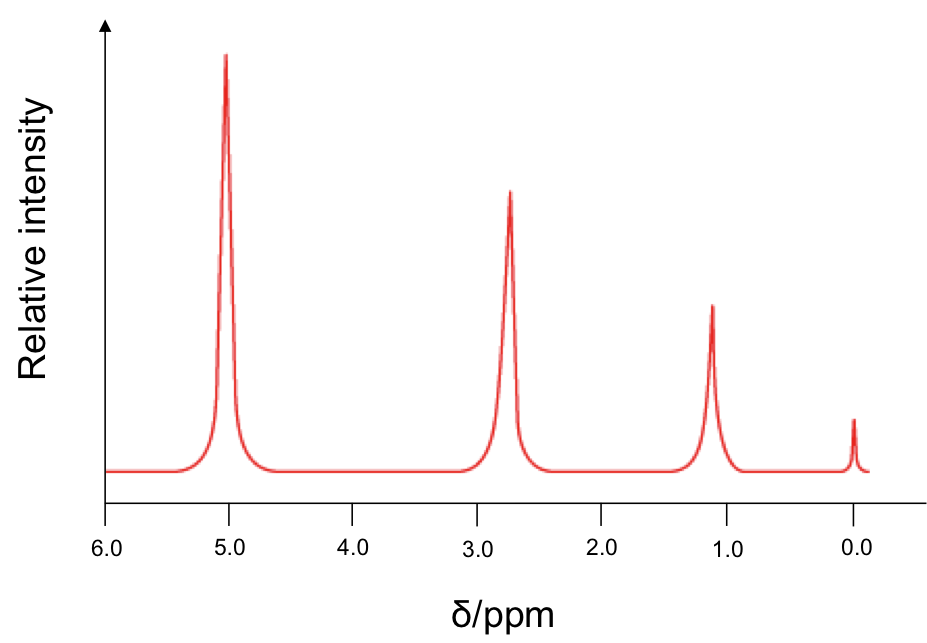
The effects of spin-spin coupling are visible on a high resolution NMR spectrum. An example is the spectrum of ethanol, CH3CH2OH:

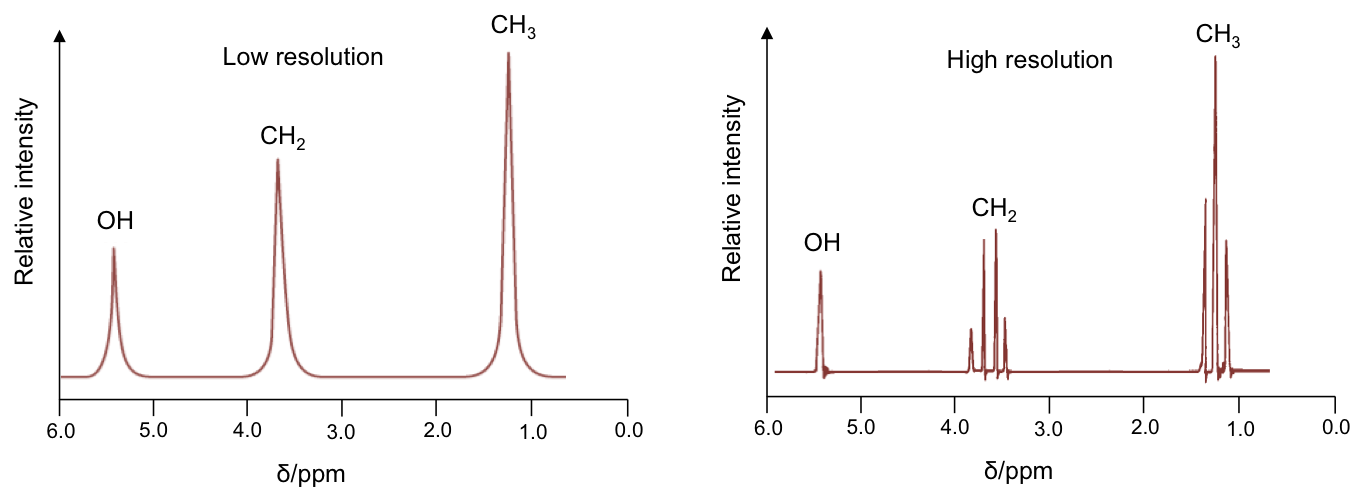
Effects of spin-spin coupling on CH3 protons

According to rule 1, the three 1Hs in the CH3 moiety are equivalent and spin-couple one another without affecting the position and shape of the CH3 peak in the spectrum. However, they are not equivalent to the two protons in CH2, which have the following possible spin orientations:

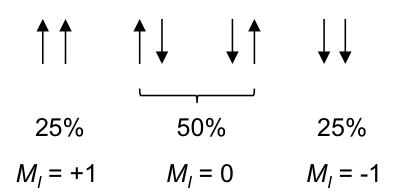
The percentages represent the statistical occurrences of the paired orientations in a sample of ethanol molecules, with MI = ΣmI , i.e. the total nuclear spin magnetic number. Depending on the spin orientation of a proton in the CH3 moiety, the paired orientations of MI = +1 or MI = -1 of protons in CH2 either shield or deshield that proton, while the paired orientations of MI = 0 in CH2 does not affect the proton’s magnetic field. The result is a splitting of the single CH3 peak into a triplet, with the middle peak retaining the same chemical shift as CH3 without spin-spin coupling effect, and an equal up and down shift for the left and right peaks. The relative intensity of the left:middle:right peaks is 1:2:1 (see high resolution diagram above).

CH3 protons are separated from the hydroxyl 1H by four bonds. So, according to rule 2, any coupling effect is negligible.

 

Effects of spin-spin coupling on CH2 protons

Using the same logic, the possible spin orientations of the three 1Hs in the CH3 moiety are:

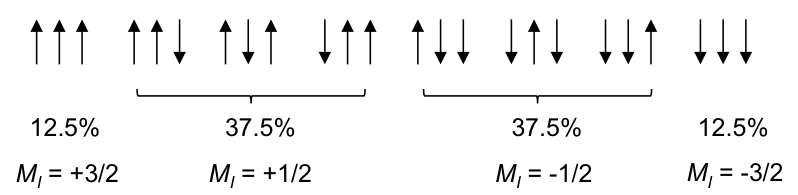
The four MI values split the single CH2 peak into a quartet, with the distribution of four peaks along a vertical line of reflection that intersects the original chemical shift of CH2 without spin-spin coupling effect. The relative intensity of the peaks is 1:3:3:1 (see high resolution diagram above).

 

Question

Why is the OH peak not a triplet and why is there no coupling effect between the hydroxyl 1H and the CH2 protons?

Answer

The presence of H3O+ or OH– in the sample, even in minute amounts, catalyses the exchange of hydroxyl protons between ethanol molecules. This exchange is fast enough to negate the spin-spin coupling effect between the hydroxyl proton and the CH2 protons. The hydroxyl protons can also be swapped with protons from H3O+, which is why the OH peak may disappear when D2O is added to the ethanol sample (ID = 0).

 

Finally, in cases where rule 3 fails, i.e. the changes in chemical shifts of spin-coupled nuclei are comparable to the difference in chemical shifts between the nuclei, the spectrum can become complex.

 

Question

Why are all peaks in a 13C NMR spectrum singlets?

Answer

13C, like 1H, has a nuclear spin of I = ½ and is expected to experience spin-spin coupling with neighbouring 13C and 1H nuclei. The natural abundance of 13C is only 1.1% and therefore the probability of a molecule having 13C adjacent nuclides is almost zero. However, 13C–1H spin-spin coupling is ubiquitous. To avoid a complicated 13C spectrum, a technique called proton decoupling is used, where protons of molecules in a sample are irradiated with a secondary radiofrequency wave. The protons undergo rapid spin reorientations that result in their net MI being zero.

 

Question

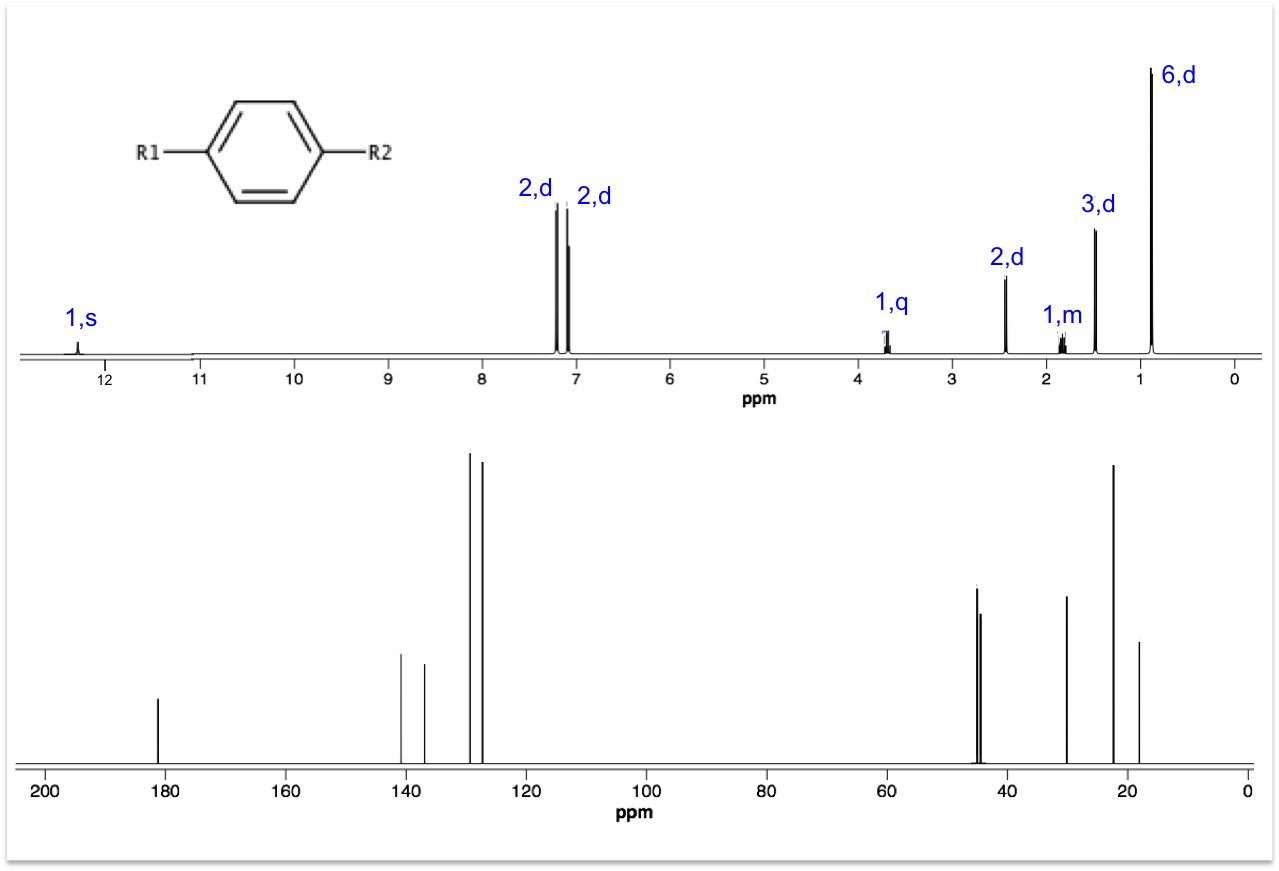
Deduce the structures for R1 and R2 using the 1H and 13C spectra below. Hint: Ar–13C 45 ppm.

Answer

Even though 13C peak areas are not a reliable indicator of the relative number of carbons, we can make a guess of the carbon numbers by comparing the peak heights. Let’s assume the three taller peaks represent two carbons each, which gives a total of 13 carbons in the molecule.

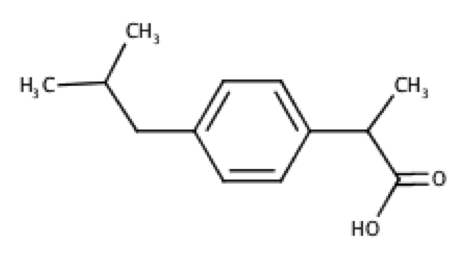
The peak at 0.90 ppm of the top spectrum is a doublet of 6 protons, which suggests an isopropyl group. The doublet of 3 protons at 1.50 ppm is mostly likely a methyl group. The singlet at 12.34 ppm is characteristic of a carboxyl proton. A pair of doublets at 7.08-7.22 ppm, each with two protons, refers to protons on the benzene ring. That leaves us with 2 carbons associated with the quartet at 3.69 ppm and the doublet at 2.45 ppm. These two carbons have almost the same chemical shift of 45 ppm in the 13C spectrum, which according to the hint are carbons adjacent to the benzene ring. Putting everything together, we have the following structure (ibuprofen):

 

Previous article: Chemical shift
Content page of nuclear magnetic resonance
Content page of intermediate chemistry
Main content page
Posted on

Chemical shift (nuclear magnetic resonance)

The chemical shift δ in nuclear magnetic resonance spectroscopy is a measure of the spin transition frequency of a nuclide with respect to a standard nuclide. It is dependent on the identity of the nuclide and the chemical environment of the nuclide. From the previous article, we learned that the concept of nuclear magnetic resonance involves analysing resonance signals of nuclides by varying an alternating electromagnetic frequency v at a constant external magnetic field B, or by varying an alternating B at a constant v. According to Lenz’s law, a changing B induces an opposite magnetic field in an electron-filled system like an atom. The magnitude of the induced magnetic field is dependent on the atom’s electron density, which is influenced by neighbouring atoms. Since this induced magnetic field is directionally opposite to the external magnetic field, the effective external magnetic field felt by the nucleus is:

B_{eff}=B-\sigma B\; \; \; \; \; \; \; \; 3

where σ is a constant called the shielding constant, which varies according to the chemical environment of an atom.

For example, 1H in the aldehyde functional group RCHO experiences a larger Beff than 1H in CH4. This is because the electropositive carbonyl carbon reduces the electron density around the hydrogen nucleus (deshield), resulting in a lower induced magnetic field when the 1H nucleus is exposed to an external magnetic field. We say that the shielding constant of 1H in the aldehyde functional group of RCHO is smaller than that of 1H in CH4, or that 1H in the aldehyde functional group of RCHO is relatively more deshielded than 1H in CH4 (note that all 1Hs in CH4 are chemically equivalent).

Substituting eq3 and the Planck relation in eq2 of a previous article, we have

v=\frac{\gamma B}{2\pi}\left ( 1-\sigma \right )\; \; \; \; \; \; \; \; 4

Eq4 shows that if B is fixed (or if v is fixed), the radiofrequency v (or the external magnetic field B) needed to stimulate a nuclear spin transition is dependent on the gyromagnetic ratio of the nuclide and the shielding constant. The remaining task is to set up a convenient measure, i.e. a scale, to represent the resonance frequencies for different nuclides. This scale, known as the chemical shift δ, is:

\delta=\frac{v-v^o}{v^o}\times 10^6\; \; \; \; \; \; \; \; 5

where vo is the resonance frequency of a reference nuclide—tetramethylsilane (TMS) with the molecular formula Si(CH3)4 is commonly used as a reference in 1H-NMR.

The reason why the fractional change term is multiplied by 106 is that the numerator is expressed in hertz, while the denominator is in megahertz. For example, the resonance frequency of 1H in TMS at a particular fixed B is 300 MHz, and that the resonance frequency of a 1H in a sample that we are investigating is 300.0003 MHz at the same B. We would expect 2 peaks in the NMR spectrum, one for the chemically equivalent 1Hs in TMS at δ = 0 (substituting v = vo in eq5), and the second peak for 1H-sample at:

\delta=\frac{300\, Hz}{300\, MHz}\times10^6=1

Since \frac{Hz}{MHz} is 1 part per million, the units for δ is ppm. Therefore, instead of plotting the horizontal axis of the NMR spectrum in Hz or MHz, we plot it in δ, which has a simpler value. A typical low-resolution spectrum looks like this:

The horizontal axis is plotted such that the more heavily shielded nuclei appear to the right of the spectrum. The small peak at 0.0 ppm corresponds to 1H from TMS. The areas under the peaks reflect the relative number of chemically equivalent 1H for the respective chemical shift.

Some common chemical shifts of 1H nuclides are as follows:

1H nuclides δ/ ppm
TMS 0.0
RCH3 0.7 – 1.2
RCH2R 1.1 – 1.5
R3CH 1.6 – 2.0
ArCH3, ArCH2R, ArCHR2 2.3 – 2.7
CH3COR 2.0 – 3.0
-OCH3, -OCH2R, -OCHR2 3.0 – 4.0
RaCHbX   where a = 0,1,2   b = 1,2,3     X = Cl, Br 3.0 – 4.2
RNH2 1.0 – 4.8
ROH 1.0 – 6.0
ArH 6.5 – 9.0
RCHO 9.5 – 10.5
RCO2H 10.0 – 13.0

13C also has a nuclear spin of ½ and is NMR active. However, a large sample is needed for analysis, as its natural abundance is about 1.1%. The typical resonance frequency of a 13C nuclide is a quarter of that of a 1H nuclide, which allows 13C spectra to be generated separately from 1H spectra. The chemical shift of 13C ranges from 0 ppm to 220 ppm. Unlike a 1H spectrum, the areas under peaks in a 13C spectrum are not a reliable indication of the relative number of carbons. This is because some carbon signals, e.g. carbonyl carbons, are weaker than other carbon signals, e.g. methyl carbons.

 

Question

Do the protons on the marked carbon have the same chemical shift?

Answer

The two protons, Ha and Hb, have different chemical shifts, as they are not equivalent (see the Newman projection below):

 

 

Next article: Spin-spin coupling
Previous article: Instrumentation
Content page of nuclear magnetic resonance
Content page of intermediate chemistry
Main content page
Posted on

Instrumentation (nuclear magnetic resonance)

A simple version of a nuclear magnetic resonance (NMR) spectrometer consists of the following:

    1. A strong magnet to provide a uniform magnetic field B (e.g. 2.35 T) to split the energy levels of nuclides in a sample.
    2. The sample in a glass tube that is rotated to allow uniform exposure to B.
    3. A coil (blue lines) connected to a radiofrequency transmitter with a varying AC voltage. The AC voltage is gradually increased during the experiment to generate electromagnetic waves of increasing frequencies.
    4. A coil wound round the sample tube and connected to a radiofrequency detector. The flipping of nuclear spins, when nuclides are excited at the appropriate electromagnetic frequencies, results in a change in magnetic dipole moment of the nuclides. This change in magnetic dipole moment induces a current in this coil, which is recorded and analysed by a computer.

Such an NMR spectrometer design, where the external magnetic field strength B is fixed while the electromagnetic radiation frequency v is varied, is called a continuous wave NMR (CW-NMR). An alternate design of a CW-NMR has a varying B and a constant v. In this design, a varying-AC coil is wound round the magnet, while a second coil with a fixed AC voltage is wrapped round the sample tube. Measurements are made for the changes in impedance (resistance of an AC circuit) of the second coil when nuclear spin transitions occur. Finally, a more sophisticated NMR spectrometer design exposes the sample to a short and intense burst of radiofrequency radiation called an electromagnetic pulse, and subsequently analyses the data using the mathematical concept of Fourier transform.

 

Next article: Chemical shift
Previous article: Nuclear magnetic dipole moment in an external magnetic field
Content page of nuclear magnetic resonance
Content page of intermediate chemistry
Main content page
Posted on

Nuclear magnetic dipole moment in an external magnetic field

We have mentioned in a quantum chemistry article that the nucleus of an atom (e.g. 1H and 13C) possesses an intrinsic angular momentum called spin I and therefore a magnetic dipole moment μ, which tends to align parallel to an external magnetic field B in two possible directions (see diagram below).

Like tiny magnets, we would expect all dipoles of a sample of nuclei to align in the direction of an external field to achieve a lower energy state. However, at room temperature, the dipoles are constantly exchanging between the two forms, to the extent that at equilibrium, there is a slight excess of nuclei with dipoles that are aligned in the direction of the field. This behaviour of nuclear magnetic dipole moments in the presence of an external magnetic field at room temperature splits the energy of nuclei EN into two levels (see diagram below).

It is found that the energy gap between the two levels ΔE is proportional to the external magnetic field:

\Delta E=\hbar \gamma B\; \; \; \; \; \; \; \; 1

where \hbar \gamma is proportionality constant, with \gamma being the gyromagnetic ratio, whose value is dependent on the identity of the nucleus.

Due to the slight excess of nuclei at the lower level at room temperature when B > 0, a net upward spin transition occurs when the nuclei are excited with radiation corresponding to ΔE. As the gyromagnetic ratio is nuclide-specific, ΔE varies for different nuclide at a fixed value of B. Furthermore, the effective external magnetic field Beff experienced by a nucleus is dependent on the magnetic environment of the nucleus, which changes eq1 to:

\Delta E=\hbar \gamma B_{eff}\; \; \; \; \; \; \; \; 2

Eq2 is the heart of the analytical technique of nuclear magnetic resonance, where the identity and location of an unknown nuclide is determined by exposing the nuclide to a constant magnetic field and subsequently detecting its transition frequency.

 

Question

What are the typical frequencies for nuclear spin transitions? Why are nuclei with I = 0 not NMR active?

Answer

The frequencies needed for nuclear spin transitions, called resonance frequencies, are in the radiofrequency range. For example, γ for 1H that is exposed to an external magnetic field of 9.4 T is 26.75 x 107 T-1s-1. Substituting these values and the Planck relation ΔE = hv in eq1, we have v = 400.2 MHz.

The formula for the change in energy of a nuclear magnetic dipole moment in the presence of a magnetic field is:

E_\pm =-m_I\hbar \gamma B

A nuclide with spin I = 0 is associated with the nuclear magnetic spin number of mI = 0, resulting in E_\pm = 0. However, a nuclide with spin I = ½ has the nuclear magnetic spin numbers of mI = +½ and mI = -½, which gives:

 

Next article: Instrumentation
Content page of nuclear magnetic resonance
Content page of intermediate chemistry
Main content page
Posted on

Nuclear spin

Nuclear spin, denoted by the symbol I, is the total spin angular momentum of the nucleus of an atom.

The nucleus, with the exception of the hydrogen nucleus, is composed of protons and neutrons. Just like the electron, both a proton and a neutron possess an intrinsic angular momentum, or spin, with a value of ½. Another similarity between protons and electrons is that protons may pair up with anti-parallel spins, which results in a net proton spin of zero for each proton pair. The ½ spin and pairing up characteristics are also inherent in neutrons.

Simplistically, we can regard nuclear spin I as the collective spins of protons and neutrons in the nucleus. Although there isn’t a formula to predict the number of proton pairs and neutron pairs in an atom, we can generalise the relationship between protons, neutrons and I as follows:

No. of protons No. of neutrons I
even even 0
odd odd 1 or 2 or 3 or…
even odd ½ or 3/2 or 5/2 or…
odd even ½ or 3/2 or 5/2 or…

For example, 17O has 8 protons and 9 neutrons. According to the table above, we would expect I_{^{17}O} = 1/2 or 3/2 or 5/2…. If 17O has 4 anti-parallel pairs of protons and 4 anti-parallel pairs of neutrons, its nuclear spin will be 1/2. However, experimental results show that I_{^{17}O} = 5/2, which means that 17O has a total of 6 pairs of protons and neutrons.

Other examples are: I_{^1H} = 1/2 (one proton) and I_{^{12}C} = 0 (6 protons and 6 neutrons). The difference in nuclear spins for 1H and 12C (and other isotopes – see table below) is exploited in an important analytical technique in chemistry called nuclear magnetic resonance.

I

 Isotopes

0

 12C, 16O

1/2

 1H, 13C, 15N, 19F, 29Si, 31P

1

2H, 14N
3/2

11B, 23Na, 35Cl, 37Cl
5/2

17O, 27Al
3

10B

Just as the electron spin quantum number s is associated with the electron spin magnetic number ms, where ms =  –s, –s + 1 …0 … s – 1, s, the nuclear spin number I is related to the nuclear spin magnetic number mI, where mI = –I, –I + 1 …0 … I – 1, I. For 1H, mI = –1/2 or mI = +1/2, i.e. 2 possible spin orientations.

 

Question

What is a boson and what is a fermion?

Answer

A boson is a particle whose total spin is an integer (0,1,2,…), while a fermion is one whose total spin is a half-integer (1/2, 3/2, 5/2,…). For example, the nuclei 12C and 16O are bosons, whereas the nuclei 17O, 27Al are fermions. Fermions are subject to the Pauli exclusion principle, which states that no two identical fermions can occupy the same quantum state. In contrast, multiple bosons can occupy the same quantum state.

 

Previous article: Heisenberg’s uncertainty principle
Content page of intermediate quantum chemistry
Content page of intermediate chemistry
Main content page
Posted on

Modern atomic structure

The earlier models of the atom were constructed using classical mechanics. When Niels Bohr introduced his model of the atom, he not only utilised Newtonian mechanics in his derivation but also incorporated the Planck relation E = hv, which was conceived a decade earlier by Max Planck, a German physicist.

In 1900, Planck was trying to develop a formula to describe the radiation spectrum of a black body when he suggested that electromagnetic radiation is a form of energy that is quantised. The significance of this concept eventually led to development of quantum theory, with Planck being regarded as the father of quantum mechanics.

Quantum mechanics is key to the elucidation of the modern structure of an atom, where electrons are no longer perceived as orbiting in defined paths around the nucleus. Instead, an atom is represented by equations that describe the probability distribution of electrons in space, giving rise to a nucleus that is surrounded by an electron cloud (see below diagram).

In the modern interpretation of the atomic structure, electrons are distributed in an atom in specific energy states that are characterised by mathematical functions known as orbitals. The maximum number of electrons that an orbital can accommodate is two (see this article for details). Orbitals with similar shapes form a sub-shell (characterised by a unique set of (n, l), e.g. px, py and pz forms the sub-shell p), and sub-shells with the same energy in the absence of an external magnetic field, constitute a shell (e.g. 2s and 2p sub-shells constitute the shell n = 2). Diagrammatically, we can describe the energy states as follows:

Mathematically, the energy states are defined by four quantum numbers, n, l, m_l and ms, as shown in the table below.

Quantum numbers

 Details

Example

Symbol

Name

Values
n Principal n\in \mathbb{Z}

n\geq 1

 Each value of n refers to a shell

n = 1 and n = 2 are the 1st shell and 2nd shell of an atom respectively.
l Angular l\in \mathbb{Z}

0\leq l\leq n-1

 Each value of l refers to a sub-shell where

\begin{matrix} \; \; \; \; \; \; \; \; \; \; \;\; l: \; \; 0\;\; 1\; \; 2\; \; 3\; ...\\ Subshell:\; s\; \; p\;\; d\; \; f\; ... \end{matrix}

For the 1st shell (n = 1), l=0, i.e. the 1st shell consists only of the sub-shell s.

For the 2nd shell (n = 2), 0\leq l\leq 1, i.e. the 2nd shell consists of two sub-shells, s and p.
m_l Magnetic m_l\in \mathbb{Z}

-l\leq m_l\leq l

with a total of 2l+1 values

 Each value of m_l refers to the orientation of an orbital in a sub-shell. The total number of m_l values in a sub-shell also refers to the total number of orbitals in that sub-shell.

For the 1st shell (n = 1), l=0, and m_l=0, with a total of one m_l value, i.e. there is only one orbital in the 1st shell.

For the s sub-shell in the 2nd shell, m_l=0 with a total of one m_l value, i.e. there’s only 1 orbital in the s sub-shell with a single orientation.

For the p sub-shell in the 2nd shell, -1\leq m_l\leq 1 with a total of three m_l values, i.e. 3 orbitals in the p sub-shell, with each orbital having a distinct orientation.
m_s Spin magnetic +\frac{1}{2} or -\frac{1}{2} Each value of m_s refers to the spin orientation of an electron.

+\frac{1}{2} refers to a spin-up electron, while -\frac{1}{2} refers to a spin-down electron

In other words, the four quantum numbers describe the energy state of an electron in an atom. The numbers are a result of many scientists’ work that were done during the early 1900s. Some of these experiments and theories that contributed to the development of quantum mechanics are listed in the table below.

Year

 Work Scientist

1900

 Planck’s law

Max Planck

1905

 Photoelectric effect

Albert Einstein

1924

 de Broglie’s hypothesis

Louis de Broglie

1925

 Schrodinger equation

Erwin Schrodinger

1925

 Pauli exclusion principle

Wolfgang Pauli

1926

 Born interpretation

Max Born
1920-1930 Aufbau principle, Madelung’s rule and Hund’s rule

Niels Bohr, Wolfgang Pauli, Erwin Madelung, Friedrich Hund

1927

 Heisenberg’s uncertainty principle

Werner Heisenberg

We shall elaborate on the above in the following articles.

 

Question

Does the energy level diagram for shells and sub-shells apply to all atoms?

Answer

The above energy level diagram is a result of the solution of the Schrodinger equation for the hydrogen atom, which has degenerate sub-shells, i.e. sub-shells belonging to a particular shell (e.g. 2s and 2p for n = 2) have the same level of energy. The degeneracy of sub-shells disappears for multi-electron atoms due to electron-electron repulsion and the shielding effect of orbitals. For a particular shell in a multi-electron atom, the smaller the angular quantum number, the lower the energy level of the sub-shell within that shell.  

 

Next article: Black body radiation
Previous article: Classical atomic theory
Content page of intermediate quantum chemistry
Content page of intermediate chemistry
Main content page
Posted on

de Broglie’s hypothesis

The de Broglie’s hypothesis states that all matter exhibits characteristics of both wave and particle. It was developed by Louis de Broglie, a French physicist, in 1924 without any experimental evidence.

What inspired him was the work of Planck and Einstein, which collectively proposed that light has the properties of a particle with a quantised energy of hv, in addition to the properties of a wave, as previously demonstrated by Thomas Young in his famous double-slit experiment.

de Broglie used Planck’s relation E = hv and Einstein’s mass-energy equivalence formula E = mc2  to establish the de Broglie relation:

hv=mc^2

hv=pc\; \; \; \; \; \; \; \; 3

where p = mc is the relativistic momentum of a photon.

Substituting the relation c = vλ in eq3:

p=\frac{h}{\lambda}\; \; \; \; \; \; \; \; 4

which is de Broglie’s relation.

de Broglie suggested that if light exhibited both wave (wavelength) and particle (momentum) characteristics, then all particles would have both properties as well. The soundness of de Broglie’s hypothesis was subsequently verified by experiments, most notably the Davisson-Germer experiment.

 

Question

Why is c = vλ?

Answer

Frequency v is the number of complete waves that passes a point per second and so, the inverse of frequency is the time for a single complete wave to pass through a point. Wavelength λ is the distance over which a complete wave repeats. Therefore, the speed of a wave is λ/(1/v) = vλ.

 

The implication of the de Broglie relation is that all matter has wave-like properties. For example, a 70kg person running with a speed of 4 m/s has a wavelength of 2.4 x 10-36 m. However, the wavelength is too small for any wave phenomena to be observed; for instance, the person does not undergo diffraction as he runs through an open door.

The de Broglie relation is a significant development in the field of quantum mechanics and is consistent with the Schrodinger equation, which quantum mechanically describes the motion of an electron in a way analogous to Newton’s laws of motion that classically describes the motion of objects.

 

Next article: davisson-Germer experiment
Previous article: Photoelectric effect
Content page of intermediate quantum chemistry
Content page of intermediate chemistry
Main content page
Posted on

Davisson-Germer experiment

The Davisson-Germer experiment studies the scattering of electrons by a nickel single crystal. In 1927, Clinton Davisson and Lester Germer, both American physicists, irradiated a nickel single crystal with a 54 eV electron beam* and rotated the detector at various angles to capture the scattered electrons (see below diagram). 

* The electron beam energy of 54 eV or 8.65 x 10-18 J is attributed to the kinetic energy of an electron (see this article for details).

Prior to the experiment, an electron is known to be a particle with a mass of 9.1 x 10-31 kg. In 1924, de Broglie hypothesised that electrons also possess wave characteristics. If so, and if electrons have wavelengths similar to the interatomic distance (or interplannar distance) of nickel in the experiment, they would be diffracted by the nickel crystal, resulting in interference patterns typically seen in Thomas Young’s diffraction experiments. 

The results indeed produced such a diffraction pattern, with a first-order constructive interference peak at φ = 50° (see diagram above). According to Bragg’s law,

2dsin\theta=n\lambda\; \; \; \; \; \; \; \; 5

where d is the interplannar distance and n is the order of diffraction.

With reference to the top diagram, \theta=90^o-\frac{\phi}{2}. Substituting \theta=90^o-\frac{50^o}{2}=65^o, the interplannar distance of Ni of 91 pm and n = 1 into eq5, results in the wavelength of the electron of λ = 165 pm.

To test de Broglie’s hypothesis, we rearrange de Broglie’s relation as follows:

\lambda=\frac{h}{p}=\frac{h}{mv}=\frac{h}{\sqrt{2m\left ( \frac{1}{2}mv^2 \right )}}=\frac{h}{\sqrt{2m(KE)}}\; \; \; \; \; \; \; \; 6

Substituting the value of the Planck constant (6.62 x 10-34 m2 kg s-1), the mass of an electron (9.1 x 10-31 kg) and kinetic energy of an electron (54 eV = 8.65 x 10-18 J ) in eq6, we get λ = 167 pm, which is in very close agreement with the experimental value of 165 pm.

The Davisson-Germer experiment therefore verifies the wave characteristic of electrons and de Broglie’s hypothesis.

Subsequently, other experiments involving other elementary particles, atoms and even macromolecules like C60 were conducted, all of which, validated de Broglie’s hypothesis. The technique employed by Davisson and Germer is now known as low energy electron diffraction (LEED), which is utilised to study surface properties of material.

Next article: Schrodinger equation
Previous article: de Broglie’s hypothesis
Content page of intermediate quantum chemistry
Content page of intermediate chemistry
Main content page
Posted on

The Born interpretation

The Born interpretation states that the probability of finding an electron of a certain quantum state around a point is proportional to the square of the modulus of the electron’s wave function \left | \psi \right |^2, which is called the probability density. It was proposed by Max Born, a German physicist, in 1926.

The amplitude of a wave function represents its magnitude, e.g. is the amplitude in the function . Since the quantum state of an electron is completely described by its wave function , which depends on the position of the electron , Born drew a parallel between the probability of finding a particle in a region of space and the intensity of a classical wave, which is proportional to the square of the wave’s amplitude.

Question

Using Hooke’s law, F = –kx, show that the intensity of a wave is proportional to the square of its amplitude.

Answer

Substituting Hooke’s law in dE = –Fdx, we have dE = kxdx (where E is energy). Integrating the simple harmonic motion over a maximum amplitude A,

E=\int_{0}^{A}kxdx=\frac{1}{2}kA^2

Since intensity I is defined as \frac{energy}{time\times area}, we have I\propto E\propto A^2 for an electromagnetic radiation falling on a particular area of a material over a certain duration.

 

Mathematically, the Born interpretation is:

\int \left | \psi \right |^2d\tau

or \int \left | \psi \right |^2d\tau=1 to ensure that the sum of individual probabilities of locating an electron over all space is normalised to one. The wave function of an electron is a complex quantity and therefore the above equation can be written as:

\int \psi^*\psi d\tau

where \psi^* is the complex conjugate of \psi.

 

Question

Why is the wave function a complex quantity? Show that \psi^*\psi=\left | \psi \right |^2.

Answer

Some differential equations are easier to solve when the function is in the complex form. This happens to be the case for the Schrodinger equation. However, only the real component is used when values of the function are compared with experimental data.

Let \psi=a+ib. So \left | \psi \right |=\sqrt{a^2+b^2}\; \; \Rightarrow \; \; \left | \psi \right |^2=a^2+b^2.

\psi^*\psi=(a-ib)(a+ib)=a^2+b^2

Therefore, \psi^*\psi=\left | \psi \right |^2 .

 

In the previous article, we mentioned that Schrodinger did not have a convincing physical interpretation of the wave function ψ, other than it being a wave equation of an electron in the atom. With the Born interpretation, the electron probability density function \left | \psi \right |^2 for a unique combination of the three quantum numbers n, l and m_l, mathematically describes an atomic orbital. When we plot the probability functions using a mathematical software, we obtain the following shapes:

These are the orbitals of a hydrogen atom.

Next article: Electron spin
Previous article: Schrodinger equation
Content page of intermediate quantum chemistry
Content page of intermediate chemistry
Main content page
Mono Quiz