To proof the Hartree equations, we begin by rearranging eq4:
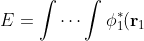\cdots\phi_n^*(\mathbf r_n)\left(-\frac{1}{2}\sum_{i=1}^n\nabla_i^2-\sum_{i=1}^n\frac{Z}{r_i}\right)\phi_1(\mathbf r_1)\cdots\phi_n(\mathbf r_n)d\tau_1\cdots d\tau_n)
\cdots\phi_n^*(\mathbf r_n)\sum_{i=1}^{n-1}\sum_{j=i+1}^n\int\frac{\vert\phi_j\vert^2}{r_{ij}}d\mathbf r_j\phi_1(\mathbf r_1)\cdots\phi_n(\mathbf r_n)d\tau_1\cdots d\tau_n\;\;\;\;\;\;\;\;(15))
Noting that  is normalised and simplifying the 1st and 2nd terms on RHS of eq15, we have
is normalised and simplifying the 1st and 2nd terms on RHS of eq15, we have
\vert\psi\right>=\sum_{i=1}^nH_i\;\;\;\;\;\;\;\;(16))
)
respectively, where \cdots\phi_n(\mathbf r_n)) ,
, \left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}\right)\phi_i(\mathbf r_i)d\mathbf r_i) , and
, and  .
.
Substituting eq16 and eq17 back in eq15, noting that  (see this article for explanation)
(see this article for explanation)
)
where E is a functional of 2n independent variables, with n variables of  and n variables of
and n variables of  .
.
To find the minimum value of E subject to n constraints of \phi_i(\mathbf r_i)d\tau_i=1) , we apply the Lagrange method of undetermined multipliers to form the new functional
, we apply the Lagrange method of undetermined multipliers to form the new functional  , where
, where
)

Question
Show that  .
.
Answer
Taking the complex conjugate of F throughout, noting that E and hence F is real (recall that the functional F is obtained by subtracting the function  , where
, where ) from E),
from E),
)
Comparing the above equation with the original F,

Substituting eq18 in  and
and  , and noting that the 2nd order terms are approximately zero,
, and noting that the 2nd order terms are approximately zero,
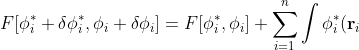\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i\right)\delta\phi_i(\mathbf r_i)d\tau_i)
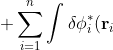\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i\right)\phi_i(\mathbf r_i)d\tau_i+\frac{1}{2}\sum_{j\neq i}\sum_{i=1}^n\int\int\delta\phi_i^*(\mathbf r_i)\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j)
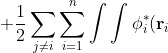\delta\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j+\frac{1}{2}\sum_{j\neq i}\sum_{i=1}^n\int\int\phi_i^*(\mathbf r_i)\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\delta\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j)
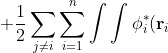\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\delta\phi_j(\mathbf r_j)d\tau_id\tau_j)
The minimum energy corresponding to F is when a small change in the functional’s input (change in  and
and  ) yields no change in the functional’s output, i.e. when
) yields no change in the functional’s output, i.e. when  , or
, or
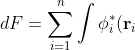\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i\right)\delta\phi_i(\mathbf r_i)d\tau_i+\sum_{i=1}^n\int\delta\phi_i^*(\mathbf r_i)\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i\right)\phi_i(\mathbf r_i)d\tau_i)
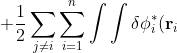\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j+\frac{1}{2}\sum_{j\neq i}\sum_{i=1}^n\int\int\phi_i^*(\mathbf r_i)\delta\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j)
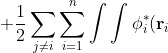\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\delta\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j)
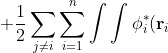\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\delta\phi_j(\mathbf r_j)d\tau_id\tau_j=0\;\;\;\;\;\;\;\;(20))

Question
Show that  is Hermitian.
is Hermitian.
Answer
Since  is Hermitian and
is Hermitian and  is real,
is real,
\psi\right]^*d\tau=\int\psi\left[\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}\right)\psi\right]^*d\tau-\varepsilon_i^*\int\psi^*\psi d\tau)
\psi d\tau-\varepsilon_i\int\psi^*\psi d\tau=\int\psi^*\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i\right)\psi d\tau)
Using the Hermitian property of the operator 
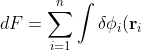\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i\right)\phi_i^*(\mathbf r_i)d\tau_i+\sum_{i=1}^n\int\delta\phi_i^*(\mathbf r_i)\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i\right)\phi_i(\mathbf r_i)d\tau_i)
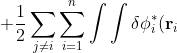\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j+\frac{1}{2}\sum_{j\neq i}\sum_{i=1}^n\int\int\phi_i^*(\mathbf r_i)\delta\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j)
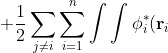\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\delta\phi_i(\mathbf r_i)\phi_j(\mathbf r_j)d\tau_id\tau_j)
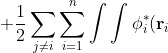\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_i(\mathbf r_i)\delta\phi_j(\mathbf r_j)d\tau_id\tau_j=0)
It can be easily shown, by expanding the Coulomb terms in the above equation, that 1st and 2nd Coulomb terms are the same, and that the 3rd and 4th Coulomb terms are the same. Therefore,
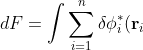\left[-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i+ \sum_{j\neq i}\int\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_j(\mathbf r_j)d\tau_j\right]\phi_i(\mathbf r_i)d\tau_i)
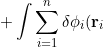\left[-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}-\varepsilon_i+ \sum_{j\neq i}\int\phi_j^*(\mathbf r_j)\frac{1}{r_{ij}}\phi_j(\mathbf r_j)d\tau_j\right]\phi_i^*(\mathbf r_i)d\tau_i=0}\;\;\;\;\;\;\;\;(20a))
) and
and ) can now be chosen arbitrarily. If we vary only the k-th function
can now be chosen arbitrarily. If we vary only the k-th function ) , eq20a becomes
, eq20a becomes
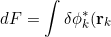\left[-\frac{1}{2}\nabla_k^2-\frac{Z}{r_k}-\varepsilon_k+ \sum_{j\neq k}\int\phi_j^*(\mathbf r_j)\frac{1}{r_{kj}}\phi_j(\mathbf r_j)d\tau_j\right]\phi_k(\mathbf r_k)d\tau_k=0})
Since ) is chosen arbitrarily, the only way to satisfy the above equation is for
is chosen arbitrarily, the only way to satisfy the above equation is for
\frac{1}{r_{kj}}\phi_j(\mathbf r_j)d\tau_j\right]\phi_k(\mathbf r_k)=0)
Similarly, if we vary only the m-th function ) , where
, where  , we have
, we have
\frac{1}{r_{mj}}\phi_j(\mathbf r_j)d\tau_j\right]\phi_m(\mathbf r_m)=0)
Repeating this logic to all other functions, we have a set of n simultaneous equations:
\frac{1}{r_{ij}}\phi_j(\mathbf r_j)d\tau_j\right]\phi_i(\mathbf r_i)=\varepsilon_i\phi_i(\mathbf r_i)\;\;\;\;\;\;\;\;(21))
and another set of n simultaneous equations in the complex conjugate form:
\frac{1}{r_{ij}}\phi_j(\mathbf r_j)d\tau_j\right]\phi_i^*(\mathbf r_i)=\varepsilon_i\phi_i^*(\mathbf r_i)\;\;\;\;\;\;\;\;(22))
Eq21 is known as the Hartree equations, and eq22, the complex conjugate form of the Hartree equations. The Hartree equations are sometimes written by changing the dummy variables  and
and  to
to  and
and  respectively. For example, eq21 can be expressed as
respectively. For example, eq21 can be expressed as
\frac{1}{\vert\mathbf r-\mathbf r'\vert}\phi_j(\mathbf r')d\tau'\right]\phi_i(\mathbf r)=\varepsilon_i\phi_i(\mathbf r))

are elements of the transformation matrix U.
is transformed to
by
. Similarly, we have
.

.