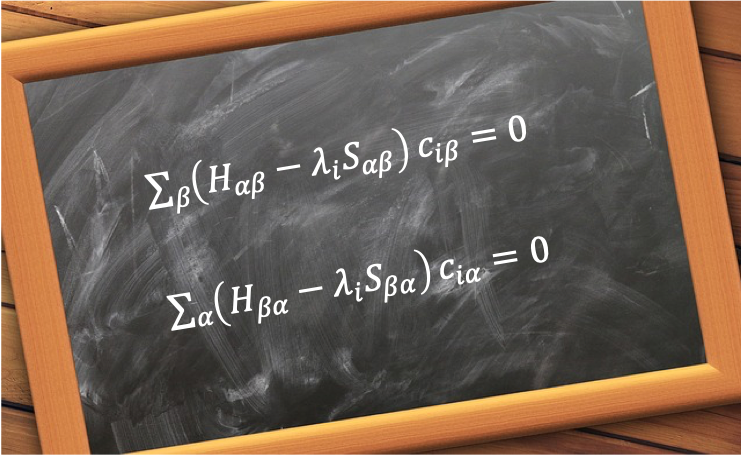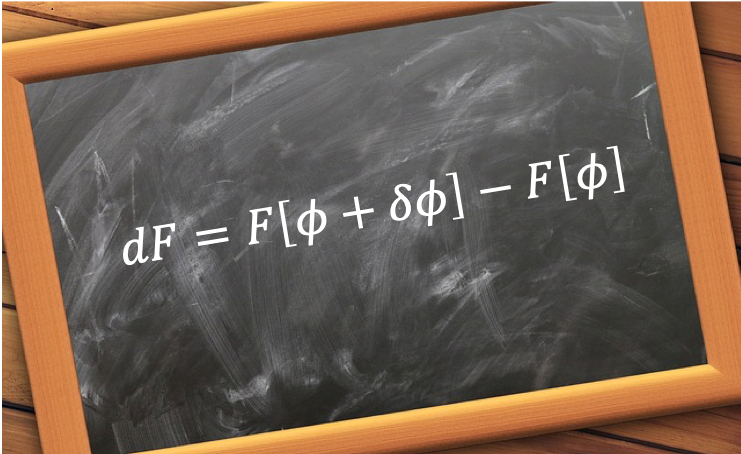As per the proof of the Hartree equations, the proof of the Hartree-Fock equations involves the use of an analogue of eq4 to find an expression similar to eq18. Applying the Lagrange method of undetermined multipliers, the resultant expression is then minimised to obtain the non-canonical form of the Hartree-Fock equations.

The analogue of eq4 is:
where is given by eq66.
Substituting eq86 and eq89 in eq93
where
Since (see this article for explanation),
For , we must have
. To find the minimum value of E subject to the constraints of
, we apply the Lagrange method of undetermined multipliers to form the new functional
, where
Substituting eq95 in eq96,
Applying the functional variation method as per the proof of the Hartree equations and noting that the minimum energy corresponding to F is when a small change in the functional’s input yields no change in the functional’s output, i.e. when or
It can be easily shown, by expanding the Coulomb and exchange terms in eq98, that the two terms within each square bracket are the same. Therefore,
where we have changed the dummy variables and
to
and
respectively.
Let’s carry out the following for the above equation:
1) Use the Hermitian property of the operator on the first term.
2) Switch the dummy indices i and j to j and i respectively for the 2nd exchange integral and the 1st undetermined multiplier term.
3) Rearrange.
The result is:

Question
Show that , i.e. the Lagrange undetermined multipliers are elements of a Hermitian matrix.
Answer
Changing the dummy variables and
of eq96 to
and
respectively and taking the complex conjugate throughout, noting that E and hence F is real (recall that the functional F is obtained by subtracting the function
, where
from E),
Using eq96 again and switching the dummy indices i and j to j and i respectively,
Comparing eq100 and eq101,
or equally
Substitute eq101a in eq99,
where
Using the same logic described in the steps taken from eq20 to eq21, we have
and its complex conjugate
Eq104 and eq105 are the Hartree-Fock equations. However, they are not in the canonical form (eigenvalue form). For the derivation of the canonical Hartree-Fock equations, see the next article.