Group theory and infra-red spectroscopy

Group theory allows us to determine the symmetries of a molecule, enabling an efficient way to obtain relevant information in infra-red (IR) spectroscopy.

The objective in this article is to use group theory to work out the symmetries of the normal modes of a molecule and then ascertain whether they are IR-active. As an example, let’s consider $H_{2}O$ , which belongs to the $C_{2v}$ point group. Here’s the corresponding character table:

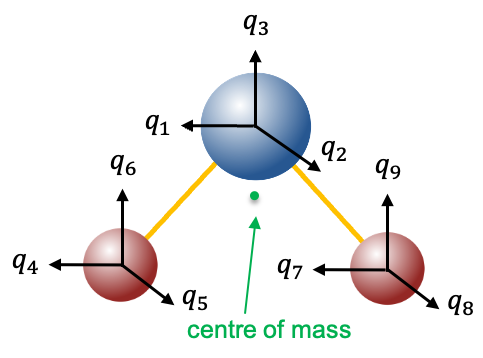
Instead of using Cartesian displacement vectors to form a basis for generating representations of the $C_{2v}$ point group, as we did in the previous article, we shall use mass-weighted Cartesian coordinate unit vectors $q_i$ to form a basis (see diagram above). Since a symmetry operation of $C_{2v}$ transforms $H_2O$ into an indistinguishable copy of itself, it transforms each of the elements of the basis set into a linear combination of elements of the set (see eq55 to eq61). Therefore, $q_i$ centred on every atom of $H_2O$ generate a representation $\Gamma_{3N}$ of the $C_{2v}$ point group. To find the matrices of the representation, we arrange the vectors into a row vector and apply the symmetry operations of the $C_{2v}$ point group on it to obtain the transformed vector. The matrices of the representation are then constructed by inspection. For example,

$q_1,q_2,q_3,q_4,q_5,q_6,q_7,q_8,q_9\)\xrightarrow{C_2}\(-q_1,-q_2,q_3,-q_7,-q_8,q_9,-q_4,-q_5,q_6$

$\begin{pmatrix}-q_1\\-q_2\\q_3\\-q_7\\-q_8\\q_9\\-q_4\\-q_5\\q_6\end{pmatrix}=\begin{pmatrix}-1&0&0&0&0&0&0&0&0\\0&-1&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0&0\\0&0&0&0&0&0&-1&0&0\\0&0&0&0&0&0&0&-1&0\\0&0&0&0&0&0&0&0&1\\0&0&0&-1&0&0&0&0&0\\0&0&0&0&-1&0&0&0&0\\0&0&0&0&0&1&0&0&0\end{pmatrix}\begin{pmatrix}q_1\\q_2\\q_3\\q_4\\q_5\\q_6\\q_7\\q_8\\q_9\end{pmatrix}$

The traces of the matrices are

Using eq27a and the character table of the $C_{2v}$ point group, we have

$A_1$	$\frac{1}{4}\[1\cdot 9+1\cdot$-1$+1\cdot 3+1\cdot 1\]=3$
$A_2$	$\frac{1}{4}\[1\cdot 9+1\cdot$-1$-1\cdot 3-1\cdot 1\]=1$
$B_1$	$\frac{1}{4}\[1\cdot 9-1\cdot$-1$+1\cdot 3-1\cdot 1\]=3$
$B_2$	$\frac{1}{4}\[1\cdot 9-1\cdot$-1$-1\cdot 3+1\cdot 1\]=2$

which implies that the decomposition of the reducible representation is $\Gamma_{3N}=3A_1\oplus A_2\oplus 3B_1\oplus 2B_2$ .

Applying the projection operator on each element of the $3N$ basis set for all irreducible representations, we have

$A_1$	$\hat{P}^{A_1}q_3=q_3$	$B_1$	$\hat{P}^{B_1}q_1=q_1$
	$\hat{P}^{A_1}q_6=\frac{1}{2}$q_6+q_9$$		$\hat{P}^{B_1}q_6=\frac{1}{2}$q_6-q_9$$
	$\hat{P}^{A_1}q_4=\frac{1}{2}$q_4-q_7$$		$\hat{P}^{B_1}q_4=\frac{1}{2}$q_4+q_7$$
	$\hat{P}^{A_1}q_9=\frac{1}{2}$q_6+q_9$$		$\hat{P}^{B_1}q_9=\frac{1}{2}$q_9-q_6$$
	$\hat{P}^{A_1}q_7=\frac{1}{2}$q_7-q_4$$		$\hat{P}^{B_1}q_7=\frac{1}{2}$q_7+q_4$$
$A_2$	$\hat{P}^{A_2}q_5=\frac{1}{2}$q_5-q_8$$	$B_2$	$\hat{P}^{B_2}q_2=q_2$
	$\hat{P}^{A_2}q_8=\frac{1}{2}$q_8-q_5$$		$\hat{P}^{B_2}q_5=\frac{1}{2}$q_5+q_8$$
	$\hat{P}^{A_2}q_8=\frac{1}{2}$q_8-q_5$$		$\hat{P}^{B_2}q_8=\frac{1}{2}$q_8+q_5$$

Each equation in the above table is a basis of the irreducible representation it belongs to. Since any linear combination of bases that transform according to a one-dimensional irreducible representation is also a basis of that irreducible representation, we can generate symmetry-adapted linear combinations (SALC) from the above basis vectors that belong to their respective irreducible representations.

We have shown in an earlier article that

1. the number of orthogonal or orthonormal basis functions of a representation corresponds to the dimension of the representation.
2. if $f_1,f_2,\cdots,f_i$ is a basis of a representation $\Gamma$ of a group, then any linear combination of $f_1,f_2,\cdots,f_i$ is a basis of a representation $\Gamma '$ that is equivalent to $\Gamma$ .

This implies that we can always select a set of nine orthonormal SALC for a block diagonal representation that is equivalent to $\Gamma_{3N}$ . Since none of the nine SALCs can be expressed as a linear combination of the others, each SALC, known as normal coordinates $Q_j$ , must describe one of nine independent motions of the molecule.

A quick method to assign the irreducible representations from the decomposition of $\Gamma_{3N}$ to the nine degrees of freedom of $H_2O$ is to refer to the character table, where the basis functions $x$ , $y$ and $z$ represent the three independent translational motion and $\boldsymbol{\mathit{R}}_x$ , $\boldsymbol{\mathit{R}}_y$ and $\boldsymbol{\mathit{R}}_z$ represent the three independent rotational motion. Deducting the irreducible representations associated with these six basis functions from the direct sum of $3A_1\oplus A_2\oplus 3B_1\oplus 2B_2$ , we are left with $A_1$ , $A_1$ and $B_1$ . These remaining three irreducible representations correspond to the vibrational degrees of freedom.

Question

Does the basis function $x$ in the character table of the $C_{2v}$ point group correspond to the normal coordinate $Aq_1+Bq_4+Cq_7$ for $H_2O$ ?

Answer

Yes. In fact, there is a correspondence between the basis functions $x,y,z,\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z$ and six of the normal coordinates of $H_2O$ . The three normal coordinates describing the vibrational motions of $H_2O$ are known as normal modes.

To verify whether the three normal modes are IR-active, we refer to the Schrodinger equation for vibration motion (see eq93):

$-\frac{\hbar^2}{2}\sum_{j=1}^m\frac{\partial^2}{\partial Q_j^2}\psi_{vib}+\frac{1}{2}\sum_{j=1}^m\lambda_jQ_j^2\psi_{vib}=E\psi_{vib}$

where the separation of variables technique allows us to approximate the total vibrational wavefunction as $\psi_{vib}=\prod_{j=1}^m\psi_j(Q_j)$ and hence, $E=\sum_{j=1}^mE_j$ .

Each $\psi_j(Q_j)$ describes a normal mode of the molecule and has the formula (see eq94):

$\psi_j(Q_j)=N_jH_j\biggr$\sqrt{\frac{\omega_j}{\hbar}}Q_j\biggr$e^{-\frac{\omega_jQ^2_j}{2\hbar}}$

where $N_j=\sqrt[4]{\frac{\omega_j}{\pi\hbar}}\frac{1}{\sqrt{2^nn!}}$ is the normalisation constant for the Hermite polynomials $H_j$ .

The total vibrational energy (see eq96) is

$E=\sum_{j=1}^m\biggr$n_j+\frac{1}{2}\biggr$\hbar\omega_j$

A vibrational state of a polyatomic molecule $\vert n_1,n_2,\cdots,n_m\rangle$ is characterised by $m$ quantum numbers. Hence, the vibrational ground state of $H_2O$ , where $m=3N-6=3$ , is $\vert 0,0,0\rangle$ or

$\vert 0,0,0\rangle=\psi_0=N\prod_{j=1}^3H_j\biggr$\sqrt{\frac{\omega_j}{\hbar}}Q_j\biggr$e^{-\frac{\omega_jQ_j^2}{2\hbar}}=N\prod_{j=1}^3e^{-\frac{\omega_jQ_j^2}{2\hbar}}$

Many IR-spectroscopy experiments are conducted at room temperature, where most molecules are in their vibrational ground state. According to the time-dependent perturbation theory, the transition probability between orthogonal vibrational states within a given electronic state of a molecule is proportional to

$\vert\langle\psi_j\vert\boldsymbol{\mathit{\mu}}\vert\psi_k\rangle\vert^2=\vert\langle\psi_j\vert\mu_x\vert\psi_k\rangle\vert^2+\vert\langle\psi_j\vert\mu_y\vert\psi_k\rangle\vert^2+\vert\langle\psi_j\vert\mu_z\vert\psi_k\rangle\vert^2\;\;\;\;\;\;\;\;104$

where $\psi_j$ and $\psi_k$ are the initial and final states respectively and $\boldsymbol{\mathit{\mu}}=\boldsymbol{\mathit{i}}\mu_x+\boldsymbol{\mathit{j}}\mu_y+\boldsymbol{\mathit{k}}\mu_z$ is the operator for the molecule’s electric dipole moment.

In other words, no transition between states occurs when $\langle\psi_j\vert\mu_x\vert\psi_k\rangle=\langle\psi_j\vert\mu_y\vert\psi_k\rangle=\langle\psi_j\vert\mu_z\vert\psi_k\rangle=0$ . Since the objective is to ascertain the IR activity of each of the three normal modes of $H_2O$ , it is suffice to study the fundamental transitions, where $\psi_j=\psi_0=\vert 0,0,0\rangle$ and $\psi_k=\vert 1,0,0\rangle$ or $\vert 0,1,0\rangle$ or $\vert 0,0,1\rangle$ .

The next step involves determining which irreducible representation of the $C_{2v}$ point group $\psi_0$ , $\psi_k$ , $\mu_x$ , $\mu_y$ and $\mu_z$ belong to. Since the components $\mu_x$ , $\mu_y$ and $\mu_z$ represent the electric dipole moment along the $x$ , $y$ and $z$ directions respectively, they transform in the same way as the basis functions $x$ , $y$ and $z$ respectively (see character table above).

Question

Show that $R_{\alpha}Q_j=\pm Q_j$ , where $R_{\alpha}$ represents the symmetry operations of a point group and $j=1,\cdots,3N-6$ .

Answer

In general, if $R_{\alpha}f(x)=f(x)$ , then the function $f(x)$ is invariant under the symmetry operation $R_{\alpha}$ . Every value of $x$ is mapped into $x$ by $R_{\alpha}$ and we can say that $R_{\alpha}x=x$ if $R_{\alpha}f(x)=f(x)$ . The converse is also true, i.e. if the variable $x$ of the function $f(x)$ transforms according to $R_{\alpha}x=x$ , then $R_{\alpha}f(x)=f(x)$ . From this article, the potential term of the vibrational Hamiltonian for $H_2O$ is ${U(Q_j)=U_e+\frac{1}{2}\sum_{j=1}^{3N-6}\lambda_jQ^2_j}$ . Since the function $U(Q_j)$ is invariant under any symmetry operation, ${U(Q_j)=U_e+\frac{1}{2}\sum_{j=1}^{3N-6}\lambda_jQ^2_j=U_e+\frac{1}{2}\sum_{j=1}^{3N-6}\lambda_j(R_{\alpha}Q_j)^2}$ or simply

$\sum_{j=1}^{3N-6}\lambda_j(R_{\alpha}Q_j)^2=\sum_{j=1}^{3N-6}\lambda_jQ_j^2\;\;\;\;\;\;\;\;105$

If each $\lambda_j$ is distinct, then $(R_{\alpha}Q_j)^2=Q_j^2$ or

$R_{\alpha}Q_j=\pm Q_j\;\;\;\;\;\;\;\;106$

If $\lambda_j$ is degenerate, eq55 states that ${R_{\alpha}Q_j=\sum_{m=1}^{k}a_{mj}Q_m$ and eq105 becomes

$\lambda_1(a_{11}Q_1+a_{21}Q_2)^2+\lambda_1(a_{12}Q_1+a_{22}Q_2)^2+\lambda_3(R_{\alpha}Q_3)^2+\cdots=\\\lambda_1Q_1^2+\lambda_1Q^2_2+\lambda_3Q_3^2+\cdots\;\;\;\;\;\;\;\;107$

where we have assumed that $Q_1$ and $Q_2$ are degenerate.

As described in this article, $Q_j$ forms a set of orthonormal eigenvectors of the vibrational Hamiltonian. So, $R_{\alpha}Q_1=a_{11}Q_1+a_{21}Q_2$ and $R_{\alpha}Q_2=a_{12}Q_1+a_{22}Q_2$ are orthonormal vectors. The matrix formed by using these vectors as its columns is an orthogonal matrix $M$ , which is defined as $M^TM=I$ . This is because the dot product of different columns will be zero, and the dot product of a column with itself will be 1. Since $M^T=M^{-1}$ if $M$ is an orthogonal matrix (see property 11 of this link for proof), $M^TM=I=MM^T$ or

$\begin{pmatrix}a_{11}&a_{21}\\a_{12}&a_{22}\end{pmatrix}\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}=\begin{pmatrix}1&0\\0&1\end{pmatrix}=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}\begin{pmatrix}a_{11}&a_{21}\\a_{12}&a_{22}\end{pmatrix}$

which implies that $a_{11}^2+a_{21}^2=a_{12}^2+a_{22}^2=a_{11}^2+a_{12}^2=a_{21}^2+a_{22}^2=1$ and $a_{11}a_{21}+a_{12}a_{22}=a_{11}a_{12}+a_{21}a_{22}=0$ .

The first two terms on LHS of eq107 then becomes $\lambda_1Q_1^2+\lambda_1Q^2_2$ . This implies that $(R_{\alpha}Q_j)^2$ must also be equal to $Q_j^2$ in eq105 if $\lambda_i$ is degenerate. Therefore, $R_{\alpha}Q_j=\pm Q_j$ regardless of whether $\lambda_i$ is non-degenerate or degenerate.

As mentioned in the above Q&A, if the variable $x$ of the function $f(x)$ transforms according to $R_{\alpha}x=x$ , then $R_{\alpha}f(x)=f(x)$ . It follows that if the variable $x$ of the function $f(x)$ transforms according to $R_{\alpha}x=-x$ , then $R_{\alpha}f(x)=f(-x)$ , in which case $R_{\alpha}$ is the reflection operator about the vertical axis of the graph of $f(x)$ against $x$ . Therefore, the ground state vibrational wave function $\psi_0$ of $H_2O$ transforms according to the totally symmetric irreducible representation $A_1$ of the $C_{2v}$ point group because

$R_{\alpha}\psi_0(Q_j)=\psi_0(\pm Q_j)=N\prod_{j=1}^3e^{-\frac{\omega_j(\pm Q_j)^2}{2\hbar}}=\psi_0$

Next, let’s analyse the symmetries of $\psi_k=\vert 1,0,0\rangle$ , $\psi_k=\vert 0,1,0\rangle$ and $\psi_k=\vert 0,0,1\rangle$ . These three wave functions (see this article) have the same form of:

$\psi_k=NQ_3\prod_{j=1}^3e^{-\frac{\omega_j Q_j^2}{2\hbar}}\;\;\;\;\;\;\;\;108$

Eq108 is a product of two functions $Q_3$ and ${\prod_{j=1}^3e^{-\frac{\omega_j Q_j^2}{2\hbar}}}$ . Since ${\prod_{j=1}^3e^{-\frac{\omega_j Q_j^2}{2\hbar}}}$ is totally symmetric, the theory of direct product representation states that $\psi_k$ must transform according to the irreducible representation of the $C_{2v}$ point group that $Q_3$ belongs to.

With reference to the $C_{2v}$ character table above, the theory of direct product representation again finds that the functions $\psi_0\mu_x$ , $\psi_0\mu_y$ and $\psi_0\mu_z$ in eq104 transform according to the irreducible representations of $B_1$ , $B_2$ and $A_1$ respectively. Therefore, the theory of vanishing integrals states that

	$\psi_k\in \Gamma_{A_1}$	$\psi_k\in \Gamma_{A_1}$
$\langle\psi_0\vert\mu_x\vert\psi_k\rangle$	Zero	Not zero
$\langle\psi_0\vert\mu_y\vert\psi_k\rangle$	Zero	Zero
$\langle\psi_0\vert\mu_z\vert\psi_k\rangle$	Not zero	Zero

Since $\vert\langle\psi_j\vert\boldsymbol{\mathit{\mu}}\vert\psi_k\rangle\vert^2\neq 0$ in eq104 for each of the three normal modes, all three normal modes of $H_2O$ are IR-active.

$A_1$	$\hat{P}^{A_1}q_3=q_3$	$B_1$	$\hat{P}^{B_1}q_1=q_1$
	$\hat{P}^{A_1}q_6=\frac{1}{2}\(q_6+q_9\)$		$\hat{P}^{B_1}q_6=\frac{1}{2}\(q_6-q_9\)$
	$\hat{P}^{A_1}q_4=\frac{1}{2}\(q_4-q_7\)$		$\hat{P}^{B_1}q_4=\frac{1}{2}\(q_4+q_7\)$
	$\hat{P}^{A_1}q_9=\frac{1}{2}\(q_6+q_9\)$		$\hat{P}^{B_1}q_9=\frac{1}{2}\(q_9-q_6\)$
	$\hat{P}^{A_1}q_7=\frac{1}{2}\(q_7-q_4\)$		$\hat{P}^{B_1}q_7=\frac{1}{2}\(q_7+q_4\)$
$A_2$	$\hat{P}^{A_2}q_5=\frac{1}{2}\(q_5-q_8\)$	$B_2$	$\hat{P}^{B_2}q_2=q_2$
	$\hat{P}^{A_2}q_8=\frac{1}{2}\(q_8-q_5\)$		$\hat{P}^{B_2}q_5=\frac{1}{2}\(q_5+q_8\)$
	$\hat{P}^{A_2}q_8=\frac{1}{2}\(q_8-q_5\)$		$\hat{P}^{B_2}q_8=\frac{1}{2}\(q_8+q_5\)$

Group theory and infra-red spectroscopy

Question

Answer

Question

Answer

Previous article: Determining the degrees of freedom of a molecule using group theory

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply

$A_1$	$\frac{1}{4}\[1\cdot 9+1\cdot\(-1\)+1\cdot 3+1\cdot 1\]=3$
$A_2$	$\frac{1}{4}\[1\cdot 9+1\cdot\(-1\)-1\cdot 3-1\cdot 1\]=1$
$B_1$	$\frac{1}{4}\[1\cdot 9-1\cdot\(-1\)+1\cdot 3-1\cdot 1\]=3$
$B_2$	$\frac{1}{4}\[1\cdot 9-1\cdot\(-1\)-1\cdot 3+1\cdot 1\]=2$