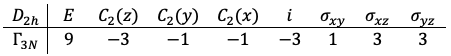Entropy is a measure of the amount of disorder or the number of possible microscopic arrangements in a system, and the arrow of time is the one-way direction in which time flows. But how are the two concepts related? To unravel this, we must first understand what entropy really is.
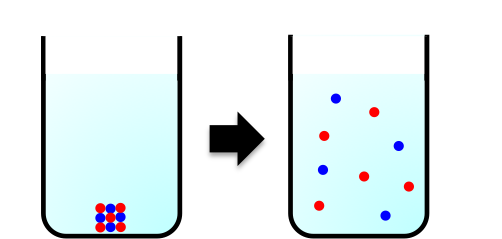
Have you ever wondered why a tablespoon of salt dissolves spontaneously in water, or why certain foods turn rancid over time? These everyday occurrences may seem unrelated, but they are all tied to a powerful concept in physics and chemistry: entropy. Though the word may conjure images of complex equations or scientific jargon, entropy is something we all experience daily. It’s the quiet force behind why hot coffee cools, why ice melts at room temperature, and even why dust spreads everywhere and instead of obediently accumulating in the dustpan.
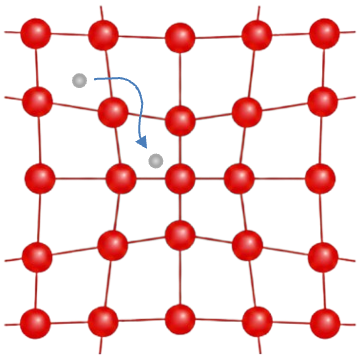
But what exactly is entropy? Many spontaneous processes that occur in our homes involve a dispersal of energy. When salt dissolves in water, the ordered solid lattice structure of sodium chloride breaks apart into freely moving ions, which can occupy many more positions within the liquid (see diagram below). Similarly, when butter turns rancid due to oxidation, gases and volatile organic compounds (such as aldehydes, ketones and short-chain fatty acids) are released, dispersing energy and matter into the surrounding air.
Entropy, denoted by 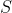 , is a measure of such energy dispersal at a specific temperature. Because spontaneous processes tend towards greater disorganisation, entropy is often loosely described as a measure of disorder or randomness in a system. In fact, the Second Law of Thermodynamics, which states that the entropy of an isolated system increases over time, is rooted in countless everyday observations like these.
, is a measure of such energy dispersal at a specific temperature. Because spontaneous processes tend towards greater disorganisation, entropy is often loosely described as a measure of disorder or randomness in a system. In fact, the Second Law of Thermodynamics, which states that the entropy of an isolated system increases over time, is rooted in countless everyday observations like these.
On closer examination, the second law is not an absolute rule but a statistical tendency that applies to systems with vast numbers of particles — atoms and molecules that move in countless ways. It describes the probabilistic tendency of these particles to evolve towards more disordered, more probable arrangements.
Consider the melting of ice at room temperature. The highly ordered crystalline structure of ice (low entropy) spontaneously transitions into liquid water (higher entropy) because there are far more ways for the molecules to arrange themselves in the fluid state than in a rigid crystal lattice. This transformation increases the total entropy of the system (ice plus water).
How then is entropy related to the arrow of time? On the macroscopic level, Newton’s equations are time-symmetric — they work just as well backward as forward. For example, if 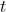 and
and  are replaced by
are replaced by  and
and  in Newton’s second law
in Newton’s second law  , the same valid solution is obtained. But when we consider systems with enormous numbers of particles, like salt dissolving in water or ice melting, the laws of probability take over. The number of possible disordered (high-entropy) configurations vastly exceeds the number of ordered (low-entropy) ones. Thus, while nothing in the laws of physics forbids entropy from decreasing, it is astronomically unlikely. In other words, entropy increases not because it must, but because it is overwhelmingly probable that it will. This statistical bias gives rise to what physicist Arthur Eddington famously called the Arrow of Time. The arrow points in the direction of increasing entropy, defining the “forward” direction of time that we perceive in memory, causality and the evolution of the universe.
, the same valid solution is obtained. But when we consider systems with enormous numbers of particles, like salt dissolving in water or ice melting, the laws of probability take over. The number of possible disordered (high-entropy) configurations vastly exceeds the number of ordered (low-entropy) ones. Thus, while nothing in the laws of physics forbids entropy from decreasing, it is astronomically unlikely. In other words, entropy increases not because it must, but because it is overwhelmingly probable that it will. This statistical bias gives rise to what physicist Arthur Eddington famously called the Arrow of Time. The arrow points in the direction of increasing entropy, defining the “forward” direction of time that we perceive in memory, causality and the evolution of the universe.
If the arrow of time points in the direction of increasing entropy, then it must have had a beginning — a moment when entropy was at its lowest. To understand the flow of time in the universe, we must look back to its earliest moments: the Big Bang.
At first glance, the Big Bang might not seem like a low-entropy event. After all, the early universe was extremely hot, dense, and filled with high-energy radiation — conditions we might intuitively associate with disorder. But entropy is not just about temperature; it also depends on how matter and energy are arranged. The early universe, though energetic, was remarkably smooth and uniform, with matter and radiation spread almost evenly in all directions. This evenness means it had very few possible configurations, and therefore, very low entropy.
The evidence for this comes from the cosmic microwave background (CMB), the faint afterglow of the Big Bang. Unlike radiation from stars or galaxies, the CMB is remarkably uniform in all directions. Observations of the CMB across the sky, interpreted using the Planck radiation law, reveal temperature variations of only about one part in 100,000. This extraordinary uniformity indicates that, in its infancy, the universe was astonishingly smooth and ordered. Had the universe begun in a random, high-entropy state, matter and radiation would have been far clumpier and more chaotic, and the arrow of time, the steady progression towards greater disorder, might never have emerged as we observe it.
As the universe expanded from the Big Bang, gravity began to play an increasingly important role in shaping entropy. Unlike most physical systems, gravity behaves counterintuitively with respect to order and disorder. In an ordinary gas, for example, molecules spread out to maximise entropy. But in a gravitational system, clumping actually increases entropy.
To see why, imagine a cloud of gas floating in space. If left alone, gravity will cause it to collapse and form a star or planet. The resulting structure seems more ordered, but in reality, the overall entropy has increased. That’s because the gravitational potential energy lost during collapse is converted into heat and radiation, which disperse into space. The final configuration, a hot star emitting light, represents a far greater number of microscopic possibilities than the original, uniform gas cloud.
This process explains how the universe could start with low entropy and still give rise to the complex, structured cosmos we see today — galaxies, stars, planets and eventually life. As gravity amplified tiny irregularities in the early universe, matter clumped together and entropy grew. The formation and evolution of stars, black holes and galaxies are all milestones on this cosmic journey towards higher entropy.
If entropy keeps increasing, what happens in the end? The answer depends on how the universe evolves, whether it will expand forever, halt and contract, or oscillate in cycles. These possibilities are described in four scenarios:
-
- Big Freeze (or heat death):
Observations over the past two decades, particularly of distant supernovae and the cosmic microwave background, reveal that the universe’s expansion is accelerating. In this case, the universe will grow ever colder and more diffuse. Over trillions of years, stars will burn out, stellar remnants will cool, and galaxies will fade into darkness. Eventually, the cosmos will approach a state of maximum entropy — a condition known as the heat death of the universe. At that point, the universe will be a thin, uniform haze of particles and radiation, with no free energy left to drive physical processes or sustain life. In such a state, the universe reaches thermodynamic equilibrium, and with no further increase in entropy possible, the arrow of time would effectively lose its direction.
-
If gravity were strong enough, it could eventually halt the expansion of the universe and reverse it into a contraction, ending in what is known as a “Big Crunch.” In this scenario, galaxies and stars would merge, black holes would coalesce, and even atoms would be torn apart as the universe collapses into an increasingly dense and hot state. The gravitational collapse releases potential energy as heat and radiation, driving the total entropy of the universe ever higher. As densities and temperatures approach extreme values, known laws of physics break down, and space and time themselves may lose their classical meaning.
-
The Big Bounce is a speculative but fascinating alternative to both the Big Freeze and Big Crunch scenarios. It proposes that the universe did not begin from a singular, one-time Big Bang, but rather from the collapse of a previous universe. In this picture, the cosmos undergoes a perpetual cycle of expansion and contraction — each “Big Crunch” giving rise to a new “Big Bang.” Instead of a final end, the universe continually renews itself through an endless series of bounces. This idea is based on the hypothesis that at extremely high densities, quantum effects could generate a repulsive force that halts the collapse before a singularity forms.
However, the Big Bounce faces a fundamental challenge from the Second Law of Thermodynamics. Entropy can only increase, so if each cycle carries forward the entropy produced in the previous one, the total disorder of the universe would accumulate from bounce to bounce. Over many iterations, the universe would grow larger and last longer with each cycle, trending towards a maximum entropy state, which leads to a heat-death-like equilibrium even within this cyclic framework. In other words, while a Big Bounce could prevent a singular end, it may not fully escape the thermodynamic arrow of time.
-
The Big Rip is one of the most dramatic and unsettling possibilities for the fate of the universe. In this model, the universe, fuelled by dark energy, keeps accelerating until it overcomes all other forces. First, distant galaxies would drift out of view as their light can no longer reach us. Then, the gravitational bonds holding galaxies together would fail. Stars and planets would be torn from their orbits, followed by the disintegration of solar systems and the destruction of individual stars. In the final moments, even atoms and subatomic particles would be ripped apart as the fabric of space itself expands faster than light can travel. The entire process would culminate in a singular event when spacetime and all known structures are shredded into oblivion.
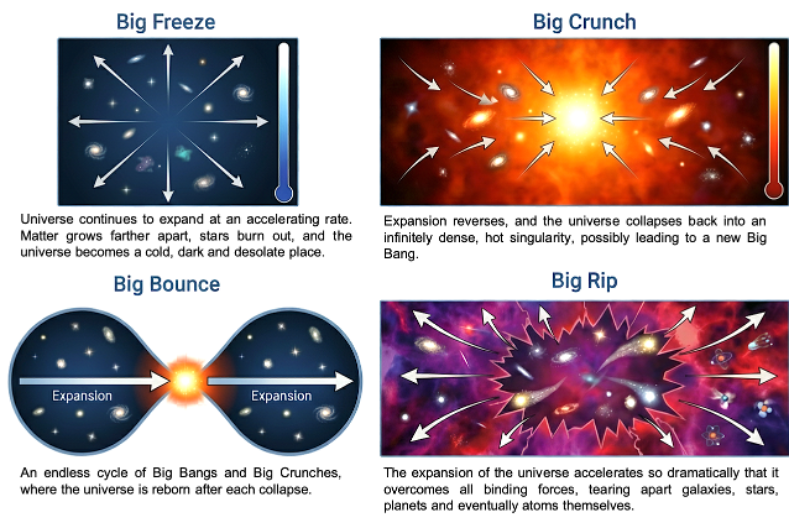
Of all the scenarios, the Big Freeze is consistent with many observations of accelerated expansion. In this case, time unquestionably continues, but it leads to a static, featureless epoch where there is no change and thus no discernible arrow of time. However, recent evidence suggesting that the universe may be decelerating raises the possibility of a Big Crunch.
Whatever the ultimate explanation, one fact remains: we live in a universe where entropy increases, where time moves inexorably forward, and where each passing moment marks a small but irreversible step in the great unfolding of cosmic history. The arrow of time, born in the furnace of the Big Bang, continues to guide the evolution of everything, from the orbits of galaxies to the beating of our own hearts.
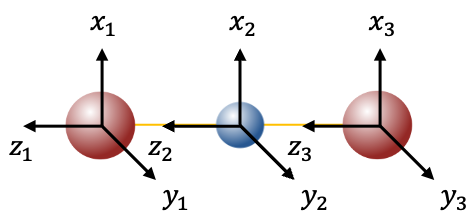
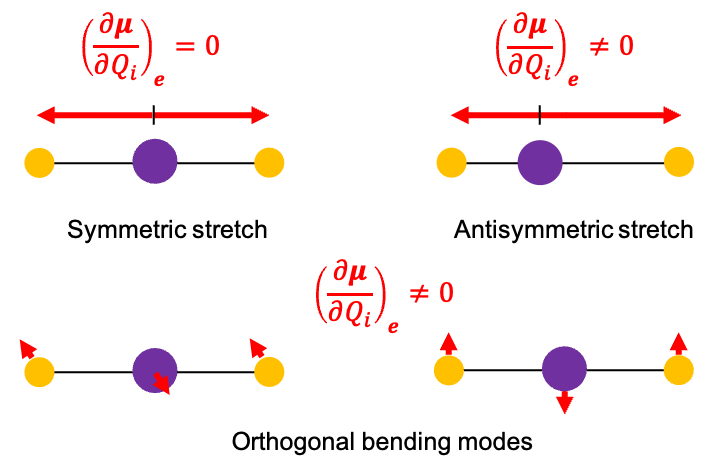
-plane belongs to the
point group. Two of its three normal modes (symmetric stretch and bend), as explained in an earlier article, transform according to the
irreducible representation, while the remaining one (asymmetric stretch) transforms according to
.

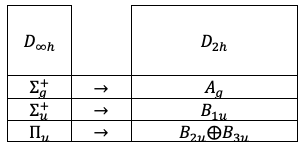
character table (see above table) shows that the linear functions (or Cartesian coordinates)
and
also transform according to
and
respectively. This correspondence means that the collective atomic displacements associated with each of the three H2O normal modes transform in the same way under the symmetry operations of the group as the corresponding Cartesian vector component.
,
and
. If a normal mode transforms according to the same irreducible representation as one of these components, then the corresponding component of the dipole moment changes as the atoms are displaced from their equilibrium positions.
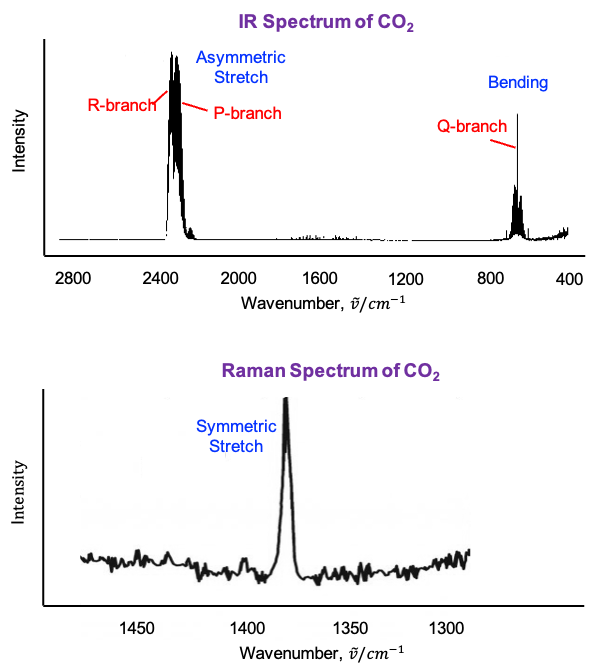
and
are IR-active.
and
modes are Raman-active.