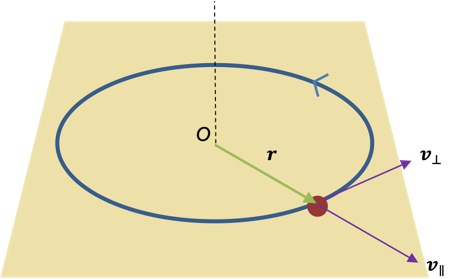
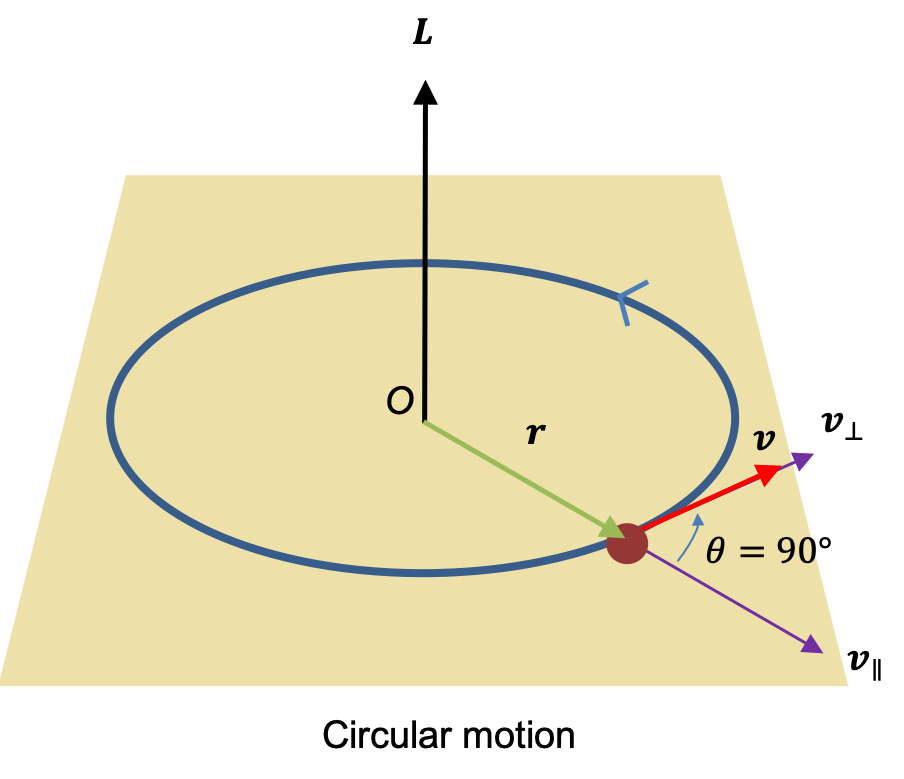
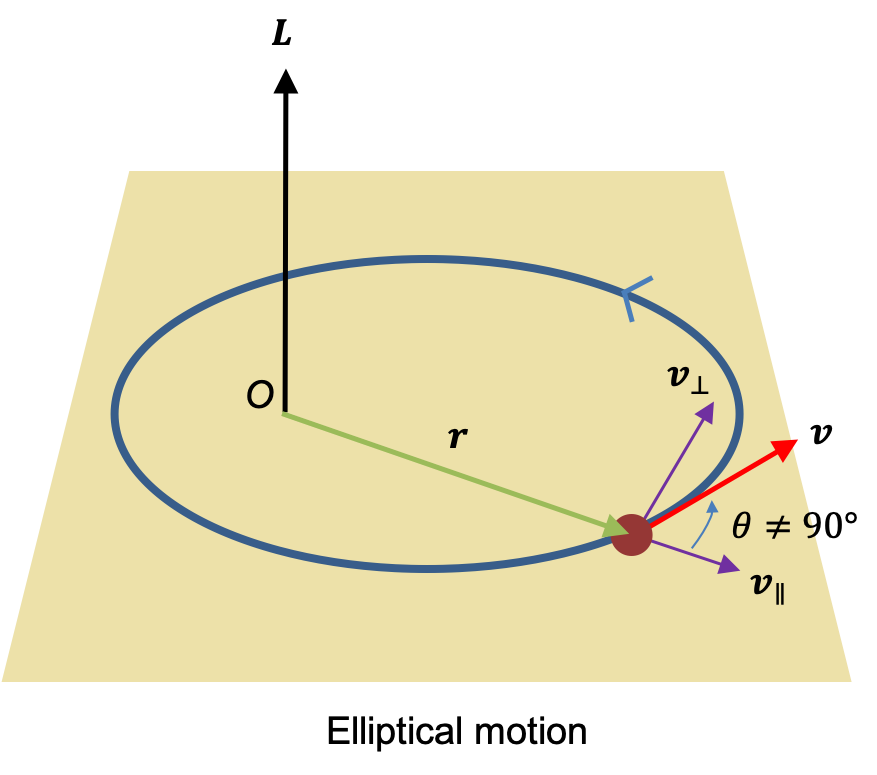
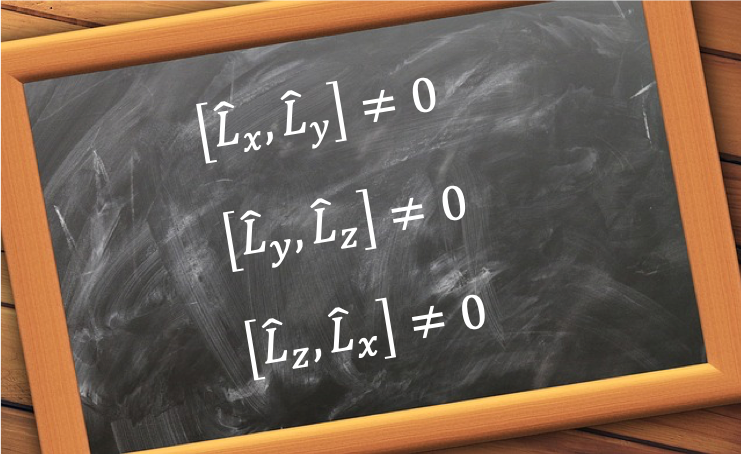The eigenvalues of quantum orbital angular momentum operators are fundamental to understanding the quantisation of angular momentum in quantum mechanics, as they dictate the allowed energy levels and spatial distributions of particles in atomic and molecular systems.
As mentioned in an earlier article, if ![\small \left [ \hat{L}^{2},\hat{L}_z \right ]=0](https://latex.codecogs.com/gif.latex?\small&space;\left&space;[&space;\hat{L}^{2},\hat{L}_z&space;\right&space;]=0)
, a common complete set of eigenfunctions can be selected for the two operators. Let 
be the common set of normalised eigenfunctions with eigenvalues 
and 
for 
and 
respectively.
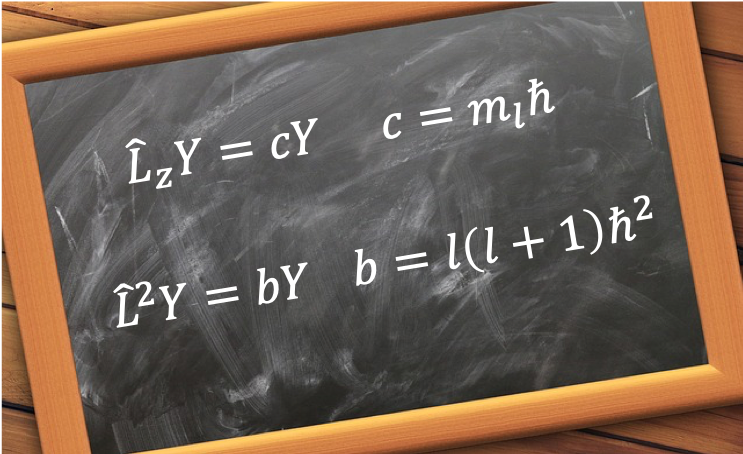
From eq75,
Multiplying the above equation by on the right, 
on the left and integrating over all space, we have
Even though is not an eigenfunction of 
, we can still find the expectation value of , which is
d\tau=\int&space;(\hat{L}_xY)(\hat{L}_xY)^{*}d\tau=\int&space;\vert&space;\hat{L}_xY\vert^{2}d\tau\geq&space;0)
Note that we have used the fact that 
is Hermitian for the 2nd equality (see eq37). Similarly, 
. So,
Therefore, has an upper bound and a lower bound. Since the eigenvalues of has an upper bound and a lower bound, from eq113 and eq114 we have
where 
, 
, 
and 
.
If we operate on eq122 with 
, we supposedly have
=(c_{max}+\hbar)(\hat{L}_+Y_{max}))
However, the above equation contradicts the upper bound eigenvalue of of 
. This implies that we must truncate the ladder beyond eq122. Since 
, we must have
Using the same argument when operating on eq123 with 
, we have
If we further operate on eq124 with , we have
Substitute eq116 in the above equation,
Y_{max}=0)
Using eq119 where 
, and eq122,
Y_{max}=0)
Since 
Similarly, operating on eq125 with and using eq115, eq119 and eq123, we have
Subtracting eq127 from eq126, we have (c_{min}-c_{max}-\hbar)=0)
. Since 
and <&space;0)
, we have 
or
As we know from eq122 and eq123, the value of 
of a particular system is dependent on the number of consecutive operations on 
by or , with each operation raising or lowering the eigenvalue of by 
. Therefore,
where 
Substituting eq128 in eq129, we have 
and 
. Therefore, the eigenvalues of are
\hbar,(-l+2)\hbar,\cdots,l\hbar)
where 
.
Substituting in eq127,
\hbar^{2}\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;131)
where .
As mentioned in the previous article, the raising and lowering operators also apply to the spin angular momentum 
and the total angular momentum 
. We would therefore expect the eigenvalues of 
and 
to be \hbar^{2})
and 
respectively, and the eigenvalues of 
and 
to be \hbar^{2})
and 
respectively. However, the quantum numbers 
and 
for the orbital angular momentum 
, but not the quantum numbers for and , are restricted to integers. Therefore,
Question
Why are the quantum numbers for restricted to integers?
Answer
The eigenvalue equation for (see eq95) is:
where 
.
Since 
must be single-valued,
})
The solution to the above equation is 
. Furthermore, is also an integer because . In other words, there are 
values of 
for a given value of 
.
We would arrive at the same results (eq130 and eq131) if we have chosen or 
instead of . The significance of eq130 and eq131 is that we can simultaneously assign eigenvalues of and (or and or and ) if the 2 operators commute. This, together with the fact that any pair of component angular momentum operators does not commute, implies that we cannot simultaneously specify eigenvalues of and more than one component angular momentum operators.
In conclusion, substituting eq130 in eq112 and eq131 in eq117
\hbar^{2}&space;Y\;\;\;\;\;\;\;\;131a)
Since is a function of and , we can express the above eigenvalue equations as:
\hbar^{2}&space;\vert&space;l,m_l\rangle&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;133)
