Advanced Chemistry - Mono Mole

July 14, 2022January 20, 2026

Composite systems (quantum mechanics)

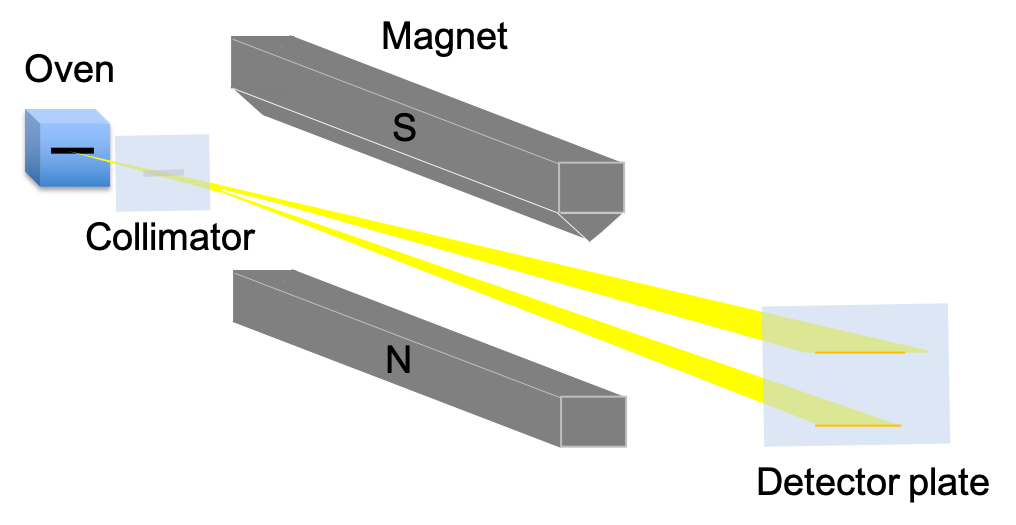
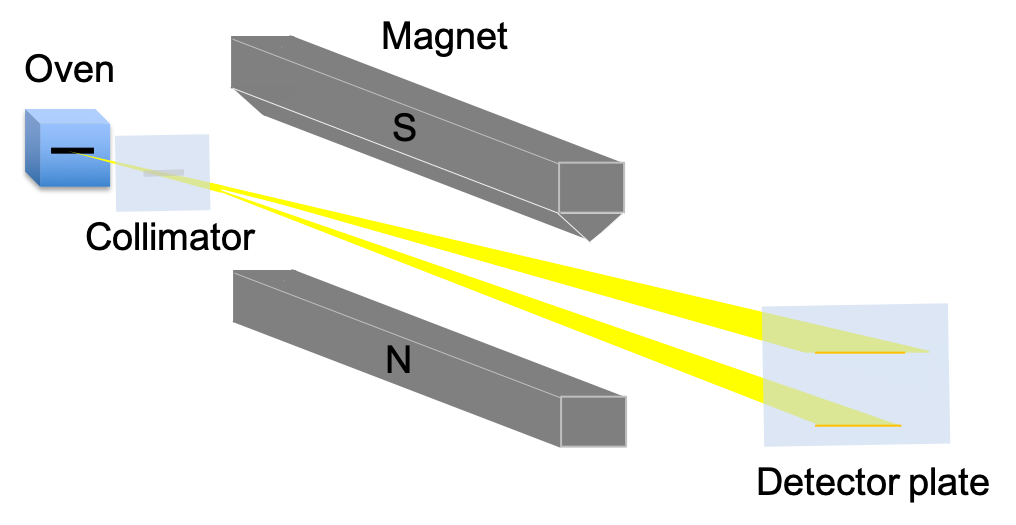
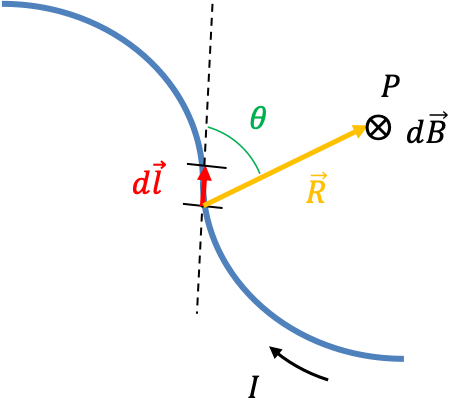
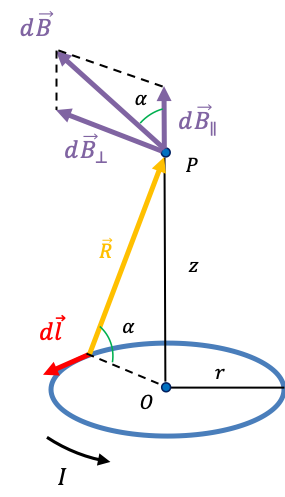
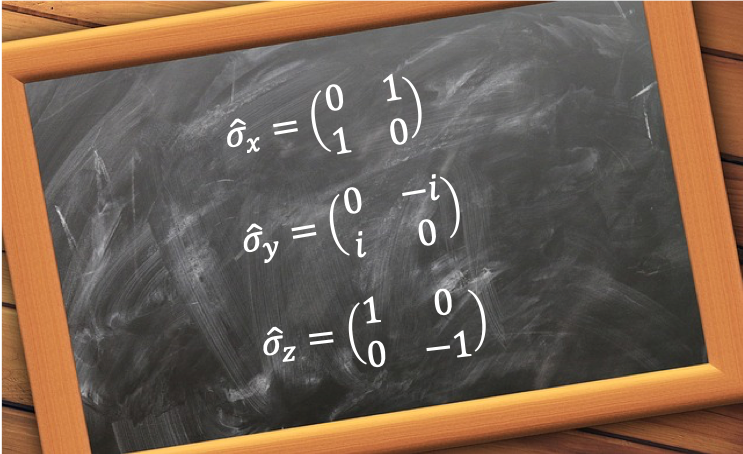A composite system is one that has more than one part; for instance, a system of two spin- $\frac{1}{2}$ particles. One possible way to denote a basis set for the eigenstates of the two spin- $\frac{1}{2}$ particles system is:

$\uparrow\uparrow\; \; \; \; \uparrow\downarrow\; \; \; \; \downarrow\uparrow\; \; \; \; \downarrow\downarrow$

or in terms of the $z$ -component of the spins:

$\vert +z,+z\rangle\; \; \; \;\vert +z,-z\rangle\; \; \; \;\vert -z,+z\rangle\; \; \; \;\vert -z,-z\rangle$

where the 1^st term and 2^nd term in the each basis state refer to the $z$ -component spin states of the 1^st particle and that of the 2^nd particle, respectively.

The full notation of $\vert +z,+z\rangle$ is $\vert s=\frac{1}{2},m_s=\frac{1}{2};s=\frac{1}{2},m_s=\frac{1}{2}\rangle$ , which can be condensed to $\vert m_s=\frac{1}{2},m_s=\frac{1}{2}\rangle$ , or simply $\vert +z,+z\rangle$ .

To represent the 4 kets in column vector form, we borrow the notation of basis vectors that are used to derive the Pauli matrices and give the kets the following assignments:

$\vert +z,+z\rangle=\begin{pmatrix} 1\\0 \\0 \\ 0 \end{pmatrix} \; \; \; \;\vert +z,-z\rangle=\begin{pmatrix} 0\\1 \\0 \\ 0 \end{pmatrix}$

$\vert -z,+z\rangle=\begin{pmatrix} 0\\0 \\1 \\ 0 \end{pmatrix} \; \; \; \;\vert -z,-z\rangle=\begin{pmatrix} 0\\0 \\0 \\ 1 \end{pmatrix} \; \; \; \; \; \; \; \; 193$

If you’ve read the article on Kronecker product, you’ll realise that

$\begin{pmatrix} 1\\0 \end{pmatrix}\otimes\begin{pmatrix} 1\\0 \end{pmatrix}=\begin{pmatrix} 1\\0 \\ 0 \\ 0 \end{pmatrix} \; \; \; \;\begin{pmatrix} 1\\0 \end{pmatrix}\otimes\begin{pmatrix} 0\\1 \end{pmatrix}=\begin{pmatrix} 0\\1 \\ 0 \\ 0 \end{pmatrix}$

$\; \; \; \;\begin{pmatrix} 0\\1 \end{pmatrix}\otimes\begin{pmatrix} 1\\0 \end{pmatrix}=\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix}\; \; \; \;\begin{pmatrix} 0\\1 \end{pmatrix}\otimes\begin{pmatrix} 0\\1 \end{pmatrix}=\begin{pmatrix} 0\\0 \\ 0 \\ 1 \end{pmatrix}$

Therefore,

$\vert\pm z,\pm z\rangle=\vert\pm z\rangle_1\otimes\vert\pm z\rangle_2\; \; \; \; \; \; \; \; 194$

Eq194 is called the uncoupled representation of the state of the system. The general state of the system, which is called the coupled representation, is a linear combination of the four basis states:

$\small \vert\psi\rangle=c_1\vert +z\rangle_1\otimes\vert +z\rangle_2+c_2\vert +z\rangle_1\otimes\vert -z\rangle_2+c_3\vert -z\rangle_1\otimes\vert +z\rangle_2+c_4\vert -z\rangle_1\otimes\vert -z\rangle_2\; \; \; \; \; \; 195$

where $\small c_1$ , $\small c_2$ , $\small c_3$ and $\small c_4$ are constants called Clebsch-Gordan coefficients.

Eq195 is often written in the general form:

$\small \vert J,M_J\rangle=\sum_{m_{j1}+m_{j2}=M_J}C_{j_1,m_{j1};j_2,m_{j2}}^{JM_J}\vert j_1,m_{j1};j_2,m_{j2}\rangle$

Question

Why is eq194 the uncoupled representation, while eq195 is the coupled representation? Why is $\small m_{j1}+m_{j2}=M_J$ ?

Answer

The $\small z$ -component of the spins in the basis vectors $\small \vert\pm z\rangle_1$ and $\small \vert\pm z\rangle_2$ that form the state $\small \vert\pm z,\pm z\rangle$ in eq194 are assumed to behave independently (non-interacting), whereas the state $\small \vert\psi\rangle$ in eq195 takes into account the coupled interactions of the spins. For example, the coupled representation is used for the singlet and triplet states (interacting spins), while both the coupled and uncoupled representations are utilised in deriving atomic term symbols where spin-orbit coupling is neglected.

In terms of $\small m_{j1}+m_{j2}=M_J$ , see the derivation of eq207 for explanation.

Consider the Hilbert spaces $\small H_1$ and $\small H_2$ that are spanned by the basis states $\small \begin{pmatrix} 1\\0 \end{pmatrix}_1,\begin{pmatrix} 0\\1 \end{pmatrix}_1$ and $\small \begin{pmatrix} 1\\0 \end{pmatrix}_2,\begin{pmatrix} 0\\1 \end{pmatrix}_2$ respectively. The Hilbert space of the composite system of the two spin- $\small \frac{1}{2}$ particles is the Kronecker product of $\small H_1$ and $\small H_2$ , i.e. $\small H_1\otimes H_2$ . To construct a total spin angular momentum operator for $\small H_1\otimes H_2$ , we have to consider the following:-

According to the principle of the conservation of angular momentum of a system, the total $\small z$ -component of the orbital angular momentum of a system is the sum of all $\small z$ -components of the orbital angular momentum of particles constituting the system $\small L_z=\sum_{i=1}^{n}l_{z,i}$ . The total $\small z$ -component of spin angular momentum, which is also a form of angular momentum, is postulated to be the sum of all $\small z$ -components of the spin angular momentum of particles constituting the system $\small S_z=\sum_{i=1}^{n}s_{z,i}$ .
The spin operator $\small \hat{S}_z^{\; (1)}$ that acts on eigenstates in the Hilbert space $\small H_1$ , and the spin operator $\small \hat{S}_z^{\; (2)}$ that acts on eigenstates in the Hilbert space $\small H_2$ , are 2×2 matrices.
The eigenvectors in $\small H_1\otimes H_2$ are column vectors with 4 elements, and hence, the spin operator must be a 4×4 matrix.

Taking the above points in consideration, $\small \hat{S}_z^{\; (1)}$ and $\small \hat{S}_z^{\; (2)}$ acting on $\small \vert\pm z\rangle_1\otimes\vert\pm z\rangle_2$ in the Hilbert space $\small H_1\otimes H_2$ are defined as:

$\small \left ( \hat{S}_z^{\; (1)}\otimes I\right ) \left ( \vert\pm z\rangle_1\otimes\vert\pm z\rangle_2\right )=\hat{S}_z^{\; (1)} \vert\pm z\rangle_1\otimes\vert\pm z\rangle_2$

and

$\small \left (I\otimes\hat{S}_z^{\; (2)}\right ) \left ( \vert\pm z\rangle_1\otimes\vert\pm z\rangle_2\right )=\vert\pm z\rangle_1\otimes\hat{S}_z^{\; (2)} \vert\pm z\rangle_2$

respectively, where $\small I$ is the 2×2 identity matrix.

The total $\small z$ -component spin angular momentum operator $\small \hat{S}_z^{\; (T)}$ that acts on the eigenstates in the Hilbert space $\small H_1\otimes H_2$ is therefore:

$\small \hat{S}_z^{\; (T)}=\hat{S}_z^{\; (1)}\otimes \hat{S}_z^{\; (2)}\; \; \; \; \; \; \; \; 196$

Substituting eq174 into the above equation,

$\hat{S}_z^{\; (T)}=\frac{\hbar}{2}\begin{pmatrix} 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &-1 &0 \\ 0 &0 &0 &-1 \end{pmatrix}+\frac{\hbar}{2}\begin{pmatrix} 1 &0 &0 &0 \\ 0 &-1 &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &-1 \end{pmatrix}=\hbar\begin{pmatrix} 1 &0 &0 &0 \\ 0 &0 &0 &0 \\ 0 &0 &0 &0 \\ 0 &0 &0 &-1 \end{pmatrix}\; \; \; \; \; \; \; \; 197$

Similarly, from eq177

$\hat{S}_x^{\; (T)}=\frac{\hbar}{2}\begin{pmatrix} 0 &0 &1 &0 \\ 0 &0 &0 &1 \\ 1 &0 &0 &0 \\ 0 &1 &0 &0 \end{pmatrix}+\frac{\hbar}{2}\begin{pmatrix} 0 &1 &0 &0 \\ 1 &0 &0 &0 \\ 0 &0 &0 &1 \\ 0 &0 &1 &0 \end{pmatrix}=\frac{\hbar}{2}\begin{pmatrix} 0 &1 &1 &0 \\ 1 &0 &0 &1 \\ 1 &0 &0 &1 \\ 0 &1 &1 &0 \end{pmatrix}\; \; \; \; \; \; \; \; 199$

and from eq178

$\hat{S}_y^{\; (T)}=\frac{\hbar}{2}\begin{pmatrix} 0 &0 &-i &0 \\ 0 &0 &0 &-i \\ i &0 &0 &0 \\ 0 &i &0 &0 \end{pmatrix}+\frac{\hbar}{2}\begin{pmatrix} 0 &-i &0 &0 \\ i &0 &0 &0 \\ 0 &0 &0 &-i \\ 0 &0 &i &0 \end{pmatrix}=\frac{\hbar}{2}\begin{pmatrix} 0 &-i &-i &0 \\ i&0 &0 &-i \\ i &0 &0 &-i \\ 0 &i &i &0 \end{pmatrix}\; \; \; \; \; \; \; \; 200$

Next, we shall derive the matrix for $\hat{{S}^{2}}^{(T)}$ . With regard to eq196, since $s_{z,max}=S$ , $\hat{S}_{z,max}^{\;\; \; \; \; \; \; \; (1)}\otimes I+I\otimes\hat{S}_{z,max}^{\;\; \; \; \; \; \; \; (2)}$ is equivalent to $\hat{S}^{(T)}=\hat{S}^{(1)}\otimes I+I\otimes\hat{S}^{(2)}$ . Therefore,

$\hat{{S}^{2}}^{(T)}=\left ( \hat{S}^{(1)}\otimes I+I\otimes\hat{S}^{(2)} \right )^{2}=\hat{{S}^{(1)}}^{2}\otimes I+2\hat{S}^{(1)}\otimes\hat{S}^{(2)}+I\otimes\hat{{S}^{(2)}}^{2}\; \; \; \; \; \; \; \; 201$

Substitute eq173 and eq179 in eq201,

$\hat{{S}^{2}}^{(T)}=\frac{3}{2}\hbar^{2}\begin{pmatrix} 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1 \end{pmatrix}+\frac{\hbar^{2}}{2} \left ( \hat{\sigma}_x\otimes\hat{\sigma}_x+\hat{\sigma}_y\otimes\hat{\sigma}_y+\hat{\sigma}_z\otimes\hat{\sigma}_z \right ) \; \; \; \; \; \; \; \; 202$

Substitute eq180 in the above equation and simplifying,

$\hat{{S}^{2}}^{(T)}=\hbar^{2}\begin{pmatrix} 2 &0 &0 &0 \\ 0 &1 &1 &0 \\ 0 &1 &1 &0 \\ 0 &0 &0 &2 \end{pmatrix}\; \; \; \; \; \; \; \; 203$

Question

What is the formula for $\hat{S}_z^{\; T}$ that acts on the eigenstates in the Hilbert space $H_1\otimes H_2\otimes H_3$ ?

Answer

$\hat{S}_z^{\; T}=\hat{S}_z^{\; 1}\otimes I\otimes I+I\otimes\hat{S}_z^{\; 2}\otimes I+I\otimes I\otimes\hat{S}_z^{\; 3}$

Question

Show that $\hat{{S}^{2}}^{(T)}$ commutes with $\hat{S}_z^{\; (T)}$ .

Answer

Using eq196 and eq201 in simple notation, $\left [\hat{{S}^{2}}^{(T)},\hat{S}_z^{\; (T)}\right ]=\left [\hat{S}_1^{\; 2}+2\hat{S}_1\cdot\hat{S}_2+\hat{S}_2^{\; 2},\hat{S}_{1z}+\hat{S}_{2z}\right ]$ . Expanding RHS of this equation and considering the following:

Use eq179 to find expressions for $\hat{S}_1^{\; 2}$ , $\hat{S}_2^{\; 2}$ and $\hat{S}_1\cdot\hat{S}_2$ .
$\hat{S}_{1i}$ and $\hat{S}_{2i}$ , where $i=x,y,z$ , act on different vector spaces and hence they commute with each other.
$[\hat{A}\hat{B},\hat{C}]=[\hat{A},\hat{C}]\hat{B}+\hat{A}[\hat{B},\hat{C}]$ and $[\hat{A},\hat{B}]=-[\hat{B},\hat{A}]$ .
Making use of eq165, eq166 and eq167.

We have

$\left [ \hat{{S}^{2}}^{(T)},\hat{S}_z^{\; (T)} \right ]=0\; \; \; \; \; \; \; \; 204$

Next article: composite systems – beyond spin operators

Previous article: sequential stern-gerlach experiments

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

July 14, 2022April 8, 2025

Sequential Stern-Gerlach experiments

A sequential Stern-Gerlach experiment involves passing a spin- $\frac{1}{2}$ particle through multiple inhomogeneous magnetic fields, each of a certain orientation. In the first example, a beam of spin- $\frac{1}{2}$ particles, e.g. silver atoms, undergoes a first measurement as it passes through an inhomogeneous magnetic field, which is parallel to the $z$ -axis (see diagram below).

The beam is split into two, and the $S_z=\frac{\hbar}{2}$ beam is allowed to travel through another inhomogeneous magnetic field, which is also $z$ -directional (the $S_z=-\frac{\hbar}{2}$ beam is blocked). The general state $\chi$ of the valence silver electron prior to passing through the first magnetic field is given by eq171:

$\chi=c_1\alpha+c_2\beta$

where $\alpha$ and $\beta$ are basis vectors representing the electron spin eigenstates of $\vert s=1/2,m_s=1/2\rangle$ and $\vert s=1/2,m_s=-1/2\rangle$ respectively; $\vert c_1\vert^{2}$ is the probability of finding the electron with the state $\vert s=1/2,m_s=1/2\rangle$ , and $\vert c_2\vert^{2}$ is the probability of finding the electron with the state $\vert s=1/2,m_s=-1/2\rangle$ , with $\vert c_1\vert^{2}+\vert c_2\vert^{2}=1$ .

Since the direction of the first magnetic field is arbitrary assigned and the beam of silver atoms emerging from the source is not polarised, we have equal probability of silver atoms with valence electrons in each eigenstate emerging, i.e. $\vert c_1\vert^{2}=\vert c_2\vert^{2}=0.5$ . Noting the orthonormality of basis vectors, the expectation value of $S_z$ with reference to eq168 is:

$\langle S_z\rangle=\langle\chi\vert\hat{S}_z\vert\chi\rangle=\langle\sqrt{0.5}\alpha+\sqrt{0.5}\beta\vert\sqrt{0.5} \frac{\hbar}{2}\alpha+\sqrt{0.5} \left ( -\frac{\hbar}{2}\right )\beta\rangle=0$

The state $\chi$ of the valence silver electron entering the second magnetic field is $\chi=c_1\alpha+c_2\beta$ , where $\vert c_1\vert^{2}=1$ and $\vert c_2\vert^{2}=0$ . Therefore, the expectation value of $S_z$ is $\langle S_z\rangle=\frac{\hbar}{2}$ .

For the second example, the $S_z=\frac{\hbar}{2}$ beam emerging from the first magnetic field is passed through a second magnetic field that is rotated 90^o, i.e. in the $x$ -direction (see diagram below).

To determine the result of the second measurement, we must express the state of the valence electron in the $S_z=\frac{\hbar}{2}$ beam in terms of $\vert\alpha_x\rangle$ and $\vert\beta_x\rangle$ , or in general where the second magnetic field is rotated parallel to an arbitrary direction $\hat{\boldsymbol{\mathit{r}}}$ ( $\hat{\boldsymbol{\mathit{r}}}$ is the unit vector in spherical coordinates, i.e. $\hat{\boldsymbol{\mathit{r}}}=sin\theta cos\phi\boldsymbol{\mathit{i}}+sin\theta sin\phi\boldsymbol{\mathit{j}}+cos\theta \boldsymbol{\mathit{k}}$ ), in terms of $\vert \alpha\rangle_{\hat{\boldsymbol{\mathit{r}}}}$ and $\vert \beta\rangle_{\hat{\boldsymbol{\mathit{r}}}}$ .

Question

How do we derive the unit vector $\hat{\boldsymbol{\mathit{r}}}$ in spherical coordinates?

Answer

Substitute eq77 in the definition of a unit vector,

$\hat{\boldsymbol{\mathit{r}}}=\frac{\boldsymbol{\mathit{r}}}{\left |\boldsymbol{\mathit{r}}\right |}=\frac{x\boldsymbol{\mathit{i}}+y\boldsymbol{\mathit{j}}+z\boldsymbol{\mathit{k}}}{r}=sin\theta cos\phi\boldsymbol{\mathit{i}}+sin\theta sin\phi\boldsymbol{\mathit{j}}+cos\theta\boldsymbol{\mathit{k}}\; \; \; \; \; \; \; \; 182b$

In other words, we need eq171 to be in the form:

$\chi_\alpha=c_1\alpha_{\hat{\boldsymbol{\mathit{r}}}}+c_2\beta_{\hat{\boldsymbol{\mathit{r}}}}\; \; \; \; \; \; \; \; 183$

This implies that we have to construct the operator $\hat{S}_{\hat{\boldsymbol{\mathit{r}}}}$ , which acts on the component of spin angular momentum along $\hat{\boldsymbol{\mathit{r}}}$ . To do so, we take the projection of $\boldsymbol{\mathit{S}}$ onto $\hat{\boldsymbol{\mathit{r}}}$ :

$\boldsymbol{\mathit{S}}\cdot\hat{\boldsymbol{\mathit{r}}}=(\boldsymbol{\mathit{i}}S_x+\boldsymbol{\mathit{j}}S_y+\boldsymbol{\mathit{k}}S_z)\cdot(sin\theta cos\phi\boldsymbol{\mathit{i}}+\sin\theta sin\phi\boldsymbol{\mathit{j}}+cos\theta\boldsymbol{\mathit{k}})$

$\boldsymbol{\mathit{S}}\cdot\hat{\boldsymbol{\mathit{r}}}=S_xsin\theta cos\phi+S_y\sin\theta sin\phi+S_zcos\theta$

Hence, the operator is

$\hat{S}_{\hat{\boldsymbol{\mathit{r}}}}=\hat{S}_xsin\theta cos\phi+\hat{S}_y\sin\theta sin\phi+\hat{S}_zcos\theta$

Substituting eq174, eq177 and eq178 in the above equation to further construct $\hat{S}_{\hat{\boldsymbol{\mathit{r}}}}$ in matrix form,

$\hat{S}_{\hat{\boldsymbol{\mathit{r}}}}=\frac{\hbar}{2}\begin{pmatrix} cos\theta &e^{-i\phi}sin\theta \\ e^{i\phi}sin\theta &-cos\theta \end{pmatrix}\; \; \; \; \; \; \; \; 184$

The eigenvalue equation is:

$\frac{\hbar}{2}\begin{pmatrix} cos\theta &e^{-i\phi}sin\theta \\ e^{i\phi}sin\theta &-cos\theta \end{pmatrix}\chi_\alpha=\begin{pmatrix} \lambda &0 \\ 0 &\lambda \end{pmatrix}\chi_\alpha\; \; \; \; \; \; \; \; 185$

where $\lambda$ is the eigenvalue; and the corresponding characteristic equation is:

$\frac{\hbar}{2}\begin{vmatrix} cos\theta-\lambda &e^{-i\phi}sin\theta \\ e^{i\phi}sin\theta &-cos\theta-\lambda \end{vmatrix}=0$

$\lambda=\pm\frac{\hbar}{2}\; \; \; \; \; \; \; \; 186$

Substitute eq183 and eq186 in eq185,

$\frac{\hbar}{2}\begin{pmatrix} cos\theta &e^{-i\phi}sin\theta \\ e^{i\phi}sin\theta &-cos\theta \end{pmatrix}\begin{pmatrix} c_1\\c_2 \end{pmatrix}=\pm\frac{\hbar}{2}\begin{pmatrix} 1 &0 \\ 0 &1 \end{pmatrix}\begin{pmatrix} c_1\\c_2 \end{pmatrix}$

$\begin{pmatrix} c_1cos\theta +c_2e^{-i\phi}sin\theta \\ c_1e^{i\phi}sin\theta -c_2cos\theta \end{pmatrix}=\pm\begin{pmatrix} c_1\\c_2 \end{pmatrix}\; \; \; \; \; \; \; \; 187$

So,

$c_1cos\theta +c_2e^{-i\phi}sin\theta =\pm c_1\; \; \; \; \; \Rightarrow \; \; \; \; \; c_2=c_1\frac{\pm1-cos\theta}{e^{-i\phi}sin\theta}$

Since $1-cos\theta=2sin^{2}\frac{\theta}{2}$ and $sin\theta=2sin\frac{\theta}{2}cos\frac{\theta}{2}$ , we have

$c_2=c_1e^{i\phi}\frac{sin\frac{\theta}{2}}{cos\frac{\theta}{2}}$

Substituting the above equation in $\vert c_1\vert^{2}+\vert c_2\vert^{2}=1$ and using $\vert e^{i\phi}\vert ^{2}=1$

$\vert c_1\vert^{2}=cos^{2}\frac{\theta}{2}\; \; \; \; \; \; \; \; 188$

Question

Show that $\vert e^{i\phi}\vert^{2}=1$ .

Answer

If $a,b\in \mathbb{R}$ , we have $\vert a+ib\vert=\sqrt{a^{2}+b^{2}}$ .

$\vert e^{i\phi}\vert^{2}=\vert cos\phi+isin\phi\vert^{2}=1$

Substitute eq188 in $\vert c_1\vert^{2} +\vert c_2\vert^{2}=1$

$\vert c_2\vert^{2}=sin^{2}\frac{\theta}{2}\; \; \; \; \; \; \; \; 189$

Therefore, eq183 becomes:

$\chi_\alpha=cos\frac{\theta}{2}\alpha_{\hat{\boldsymbol{\mathit{r}}}}+sin\frac{\theta}{2}\beta_{\hat{\boldsymbol{\mathit{r}}}}\; \; \; \; \; \; \; \; 190$

Note that we could have equally used $c_1e^{i\phi}sin\theta-c_2cos\theta=\pm c_2$ in eq187 to arrive at eq188 and eq189. Using eq188, the probability of measuring the $\alpha_{\hat{\boldsymbol{\mathit{r}}}=90^{\circ} }$ state is

$\vert c_1\vert^{2}=cos^{2}\frac{90^{\circ}}{2}=0.5\; \; \; \; \; \; \; \; 191$

Using eq189, the probability of measuring the $\beta_{\hat{\boldsymbol{\mathit{r}}}=90^{\circ} }$ state is

$\vert c_2\vert^{2}=sin^{2}\frac{90^{\circ}}{2}=0.5\; \; \; \; \; \; \; \; 192$

Therefore, we observe that the $S_z=\frac{\hbar}{2}$ beam is split equally into two beams by the second magnetic field. Using the same logic, the $S_x=\frac{\hbar}{2}$ beam will again split into two beams by the third magnetic field:

$\vert c_1\vert^{2}=cos^{2}\frac{270^{\circ}}{2}=0.5\; \; \; \; \; \; and\; \; \; \;\; \; \vert c_2\vert^{2}=sin^{2}\frac{270^{\circ}}{2}=0.5$

In general, the probability of observing the $\alpha_{\hat{\boldsymbol{\mathit{r}}}}$ state is depicted in the graph below.

Question

Do eq188 and eq189 apply to the output of the beam passing through the second magnetic field in the first example?

Answer

Yes. In the first example, $\vert c_1\vert^{2}=cos^{2}\frac{0^{\circ}}{2}=1$ and $\vert c_2\vert^{2}=sin^{2}\frac{0^{\circ}}{2}=0$ .

Next article: composite systems

Previous article: pauli matrices