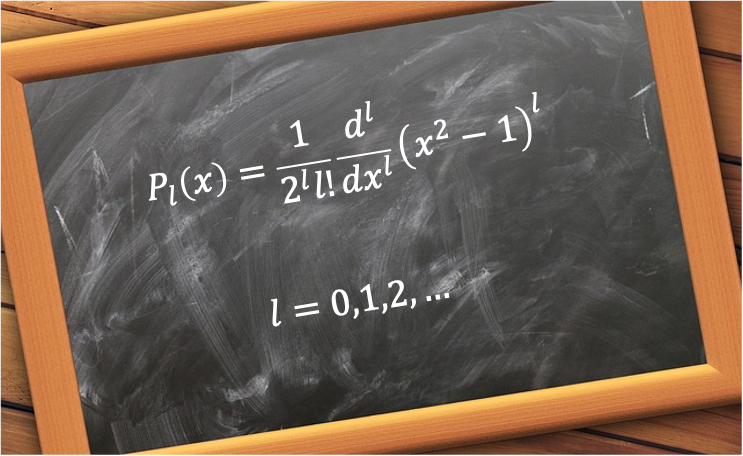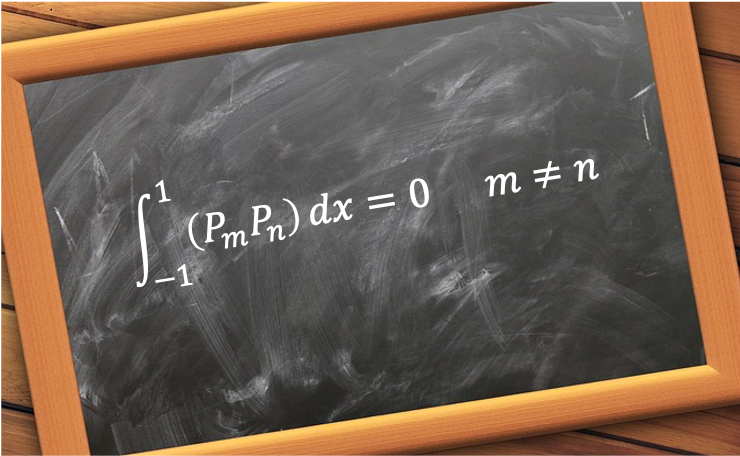Legendre polynomials 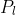 are a sequence of orthogonal polynomials that are solutions to the Legendre differential equation:
are a sequence of orthogonal polynomials that are solutions to the Legendre differential equation:
\frac{d^2P_l}{dx^2}-2x\biggr(\frac{dP_l}{dx}\biggr)+l(l+1)P_l=0\;\;\;\;\;\;\;\;332)
which can also be expressed as
\frac{dP_l}{dx}\biggr\]+l(l+1)P_l=0\;\;\;\;\;\;\;\;332a)
When 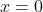 , eq332 simplifies to a form that resembles the simple harmonic oscillator equation, which has a power series solution. This implies that we can use
, eq332 simplifies to a form that resembles the simple harmonic oscillator equation, which has a power series solution. This implies that we can use =\sum_{n=0}^{\infty}a_nx^n}) to solve eq332 around
to solve eq332 around 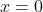 . Substituting
. Substituting  ,
, a_nx^{n-2}}) and
and a_nx^{n-2}=\sum_{n=0}^{\infty}(n+2)(n+1)a_{n+2}x^{n+2}}) in eq332 yields
in eq332 yields
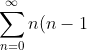a_nx^{n-2}-\sum_{n=0}^{\infty}(n+2)(n+1)a_{n+2}x^{n+2}-2\sum_{n=0}^{\infty}na_nx^{n}+l(l+1)\sum_{n=0}^{\infty}a_nx^{n}=0)
To simplify this equation, substitute  and
and  for the first sum and second sum, respectively, and then change the indices for both sums back to
for the first sum and second sum, respectively, and then change the indices for both sums back to  to give
to give
a_0+2a_2\]x^0+\[6a_3-2a_1+l(l+1)a_1\]x\\&+\sum_{n=2}^{\infty}\[(n+2)(n+1)a_{n+2}-n(n-1)a_n-2na_n+l(l+1)a_n\]x^n=0\end{align})
To satisfy the above equation for all 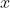 , all coefficients must be zero. Therefore,
, all coefficients must be zero. Therefore, (n+1)a_{n+2}-n(n-1)a_n-2na_n+l(l+1)a_n=0) , which rearranges to
, which rearranges to
-l(l+1)}{(n+2)(n+1)}=0\;\;\;\;\;\;\;\;333)
Eq333 is a recurrence relation. If we know the value of 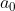 , we can use the relation to find
, we can use the relation to find  . Similarly, if we know
. Similarly, if we know 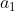 , we can find
, we can find  .
.

Comparing the recurrence relations for even  ,
,
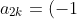^k\frac{a_0}{(2k)!}\prod_{i=0}^{k-1}\[l(l+1)-(2i+1)(2i)\]\;\;\;k=1,2,\cdots\;\;\;\;\;334)

Question
Prove that eq334 is consistent with eq333 by induction.
Answer
For 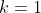 , eq334 becomes
, eq334 becomes ) , which is consistent with eq333 when
, which is consistent with eq333 when  . Let’s assume eq334 is true for
. Let’s assume eq334 is true for  , i.e.,
, i.e.,
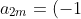^m\frac{a_0}{(2m)!}\prod_{i=0}^{m-1}\[l(l+1)-(2i+1)(2i)\]\;\;\;\;\;\;\;\;334a)
is consistent with eq333 when  .
.
We need to prove that eq334 holds for 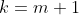 , i.e.,
, i.e.,
}=(-1)^{m+1}\frac{a_0}{\[2(m+1)\]!}\prod_{i=0}^{m}\[l(l+1)-(2i+1)(2i)\]\;\;\;\;\;\;\;\;334b)
is consistent with eq333 when  .
.
Substituting eq334a in eq334b gives eq333 when  .
.
Similarly, mathematical induction proves that the recurrence relations for odd  can be expressed as
can be expressed as
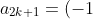^k\frac{a_1}{(2k+1)!}\prod_{i=1}^{k}\[l(l+1)-(2i+1)(2i)\]\;\;\;k=1,2,\cdots\;\;\;\;\;335)
Hence the general form of the power series is:
=&\;a_0+\sum_{k=1}^{\infty}(-1)^k\frac{a_0}{(2k)!}\prod_{i=0}^{k-1}\[l(l+1)-(2i+1)(2i)\]x^{2k}\\&+a_1x+\sum_{k=1}^{\infty}(-1)^k\frac{a_1}{(2k+1)!}\prod_{i=1}^{k}\[l(l+1)-(2i+1)(2i)\]x^{2k+1}\;\;\;\;\;336\end{align})
To see how eq336 behave for large 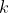 , we carry out the ratio test for the coefficients. With respect to eq333, the numerator
, we carry out the ratio test for the coefficients. With respect to eq333, the numerator -l(l+1)\approx n^2) for large
for large  . Hence
. Hence  , which implies that
, which implies that  . This means that the coefficients will not vanish as
. This means that the coefficients will not vanish as  increases. In fact, for large
increases. In fact, for large  , the behaviour of
, the behaviour of ) resembles the Taylor series expansion
resembles the Taylor series expansion  , which diverges at
, which diverges at 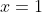 . Therefore, to ensure that
. Therefore, to ensure that ) is square-integrable, we need to truncate either one of the series after some finite terms and let all the coefficients of the other series be zero.
is square-integrable, we need to truncate either one of the series after some finite terms and let all the coefficients of the other series be zero.
To truncate either series, we let 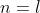 for the numerator of eq333 so that every successive term in the selected series is zero. The solution to eq332 then becomes two separate equations of eq366, each associated with one truncated series. To further show that these two equations can be combined into one, substitute
for the numerator of eq333 so that every successive term in the selected series is zero. The solution to eq332 then becomes two separate equations of eq366, each associated with one truncated series. To further show that these two equations can be combined into one, substitute 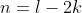 in eq333 and rearrange it to give:
in eq333 and rearrange it to give:
(l-2k+1)}{2k(2l-2k+1)}a_{l-2k+2}\;\;\;\;\;\;k=1,2,\cdots,m\;\;\;\;\;\;337)
where  for the even series and
for the even series and  for the odd series.
for the odd series.
Eq337 for some values of 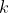 are presented in the table below. In contrast with the table above, the coefficients of eq337 are expressed in the reverse order.
are presented in the table below. In contrast with the table above, the coefficients of eq337 are expressed in the reverse order.

Comparing the recurrence relations in the above table, we have
^k}{2^kk!}\frac{l(l-1)(l-2)\cdots(l-2k+1)}{(2l-1)(2l-3)\cdots(2l-2k+1)}a_{l}\;\;\;\;\;\;\;\;338)
Since \cdots(l-2k+1)\cdots 1) , we have
, we have \cdots(l-2k+1)=\frac{l!}{(l-2k)!}) . So, eq338 becomes
. So, eq338 becomes
^k}{2^kk!}\frac{l!}{(l-2k)!(2l-1)(2l-3)\cdots(2l-2k+1)}\frac{(2l-2)(2l-4)\cdots(2l-2k)}{(2l-2)(2l-4)\cdots(2l-2k)}a_{l})
^k}{2^kk!}\frac{l!}{(l-2k)!(2l-1)(2l-3)\cdots(2l-2k+1)}\frac{2^k(l-1)(l-2)\cdots(l-k)}{(2l-2)(2l-4)\cdots(2l-2k)}a_{l}\;\;\;\;\;339)
Substituting (l-2)\cdots(l-k)=\frac{(l-1)!}{(l-k-1)!}) in eq339 yields
in eq339 yields
^k}{k!}\frac{l!}{(l-2k)!(2l-1)(2l-2)\cdots(2l-2k+1)(2l-2k)}\frac{(l-1)!}{(l-k-1)!}a_{l}\;\;\;\;\;340)
Since !=(2l-1)(2l-2)\cdots(2l-2k)\cdots 1) , we have
, we have (2l-2)\cdots (2l-2k)}=\frac{(2l-2k-1)!}{(2l-1)!}) . So eq340 becomes
. So eq340 becomes
^k}{k!}\frac{l!(2l-2k-1)!}{(l-2k)!(2l-1)!}\frac{(l-1)!}{(l-k-1)!}a_{l}\;\;\;\;\;341)
By convention, the leading coefficient is selected as !}{2^l(l!)^2}) (so that
(so that =1) ), which when substituted in eq341 gives
), which when substituted in eq341 gives
^k}{k!}\frac{(2l-2k)!}{2^lk!(l-2k)!(l-k)!})
Therefore, eq336 can be rewritten as
=\sum_{k=0}^m\frac{(-1)^k(2l-2k)!}{2^lk!(l-2k)!(l-k)!}x^{l-2k}\;\;\;\;\;\;\;\;342)
where  for even
for even 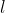 ,
,  for odd
for odd  and
and ) are known as the Legendre polynomials.
are known as the Legendre polynomials.

The first few Legendre polynomials are:
=1\\P_1(x)=x\\P_2(x)=\frac{1}{2}(3x^2-1)\\P_3(x)=\frac{1}{2}(5x^3-3x)\\P_4(x)=\frac{1}{8}(35x^4-30x^2+3)\\P_5(x)=\frac{1}{8}(63x^5-70x^3+15x)\end{multline})
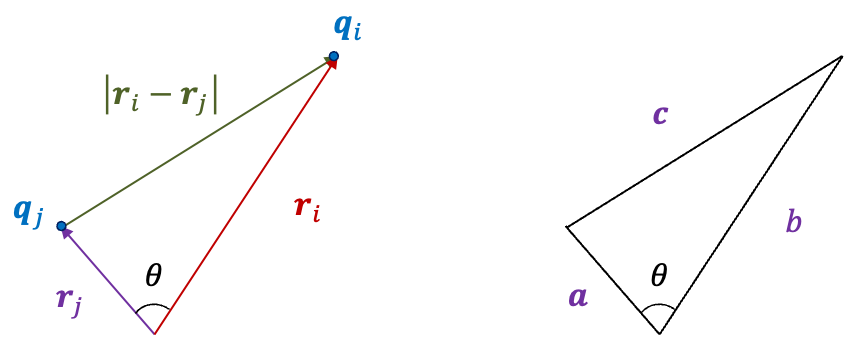
. As the two points
and the angle
between them form a triangle, the Legendre polynomials
are related to the cosine rule
, which can be rearranged to
and
.
, we have
and hence
. This implies that we can expand the RHS of eq343 as a binomial series:
are the Legendre polynomials. Therefore, the generating function
for the Legendre polynomials
is