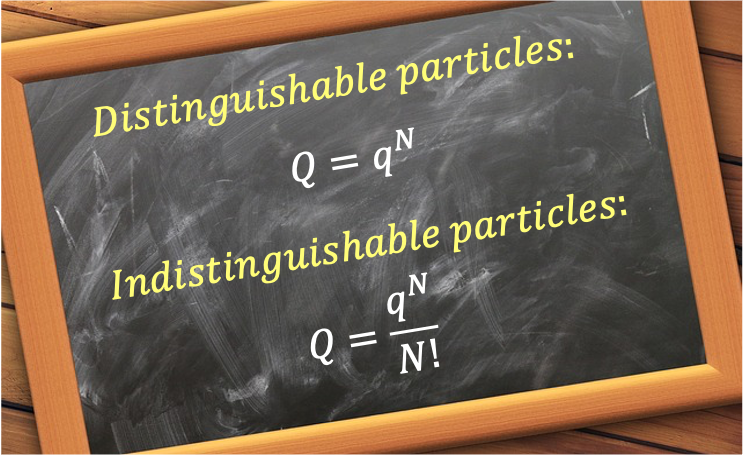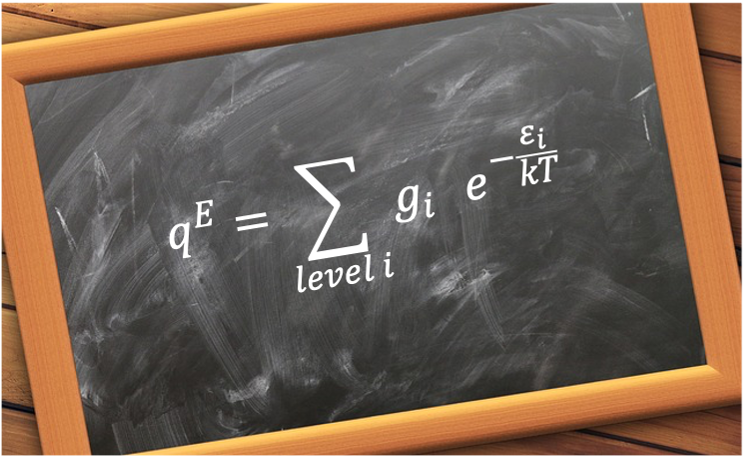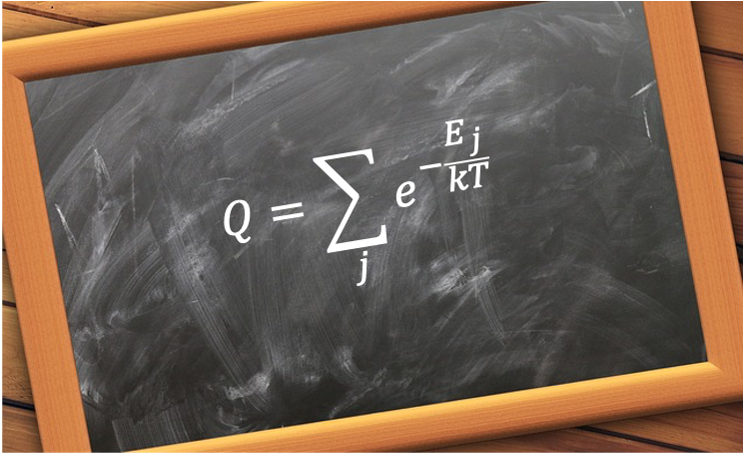A canonical ensemble is a collection of identical, non-interacting copies of a physical system, each with a fixed number of particles , fixed volume
, and constant temperature
(maintained by thermal equilibrium with a heat bath), in which particles within each system may interact.

The word “canonical” means “according to a rule”, which, in this case, refers to fixed ,
and
. As mentioned in the above definition, a canonical ensemble clearly states that even though the individual systems in the ensemble are identical from a thermodynamic perspective, they may not be identical at the molecular level. Such a theoretical construct serves to connect the microscopic behaviour of systems (governed by quantum mechanics or classical mechanics) to the macroscopic thermodynamic properties.

Question
Why do we only consider three parameters for each system?
Answer
While a physical system, such as a salt solution, may involve many microscopic variables (like individual particle positions and velocities), its macroscopic behaviour can often be fully characterised by a small set of thermodynamic parameters. In the canonical ensemble, fixing ,
and
is sufficient to statistically describe the equilibrium properties of the system.
All thermodynamic properties are, in essence, measured as averages. Consider each system in the ensemble as a rigid container holding a gas. The pressure of the gas in each system is the time average of countless rapid collisions of gas particles with the walls of the container. The force on the wall fluctuates constantly, but a pressure gauge cannot register each individual fluctuation. Instead, the gauge averages the force over a short time to provide a stable reading. Similarly, while the kinetic energy of individual molecules varies moment to moment, the temperature reflects the average kinetic energy of all molecules at thermal equilibrium.
Due to fluctuations in properties such as pressure, kinetic energy or even quantum-mechanical variables, each system can occupy many possible energy states (microstates) at any given moment. In quantum mechanical systems, the energy corresponding to each microstate is determined by solving the Schrodinger equation , where
is the wavefunction that describes the quantum state resulting from the positions and momenta of all
particles in the system, and
is the total energy of system for the
-th microstate.
If the number of systems in the ensemble is taken to be infinitely large, we postulate that:
Postulate 1
The macroscopic properties of a system are given by statistical averages over all possible microstates in the ensemble at any given moment (ensemble average).
For example, the thermodynamic internal energy is equal to the statistical average energy of the systems
in the ensemble:
where is the probability that a system in the ensemble is in the
-th microstate with energy
.
To determine , we further postulate that:
Postulate 2
All microstates with equal energy have equal probability of occurring for any system of fixed volume, composition and temperature.
Therefore, if we consider any such system in thermal equilibrium with a constant temperature heat bath, and identify two of its microstates, 1 and 2, with energies and
respectively, the corresponding probabilities are given by
and
, where
is the number of systems with energy
. It follows that the relative probability is:
In thermodynamics and quantum mechanics, energy is always referenced to a zero of energy , which can be defined in different ways. Since the function
represents a physical quantity, it must yield the same result regardless of how
is defined. This is only possible if the function
depends on the difference between
and
, i.e.
.

Question
Show that the function is invariant to
.
Answer
Let and
. We have
, which does not depend on
.
Multiplying by
and using
gives:
Letting and
, we can rewrite eq122 as:
Taking the natural logarithm on both sides of eq123 and then differentiating with respect to yields:
Using the chain rule,
Similarly, taking the natural logarithm on both sides of eq123 and then differentiating with respect to yields:
Equating eq124 and eq125 results in:
Each side of eq126 is a function of a different independent variable. The only way eq126 can be valid for all values of and
is if both functions are equal to the same constant
:
Integrating , i.e.
, gives
or equivalently,
where .
Accordingly, we have:
Substituting eq129 into yields
or:
where .
can be evaluated by summing both sides of eq130 over
:
Since ,
Substituting eq131 back into eq130 results in:
where .
Eq133 represents the general probability of finding a system, which is in thermal equilibrium with a constant temperature heat bath, in a specific microstate with energy
. Its derivation relies on fundamental principles of probability and the nature of equilibrium, not on the specific nature of the particles themselves (e.g., whether they’re distinguishable or indistinguishable). In other words, eq133 is applicable to both classical and quantum mechanical systems. Therefore, eq120 becomes:
where
is known as the canonical partition function.
The fact that eq133 yields the same expression as the Boltzmann distribution is not a coincidence. It demonstrates that the Boltzmann distribution naturally emerges from the statistical treatment of systems in thermal equilibrium, and illustrates the deep consistency between thermodynamic principles and statistical reasoning.

Question
Can two different microstates have the same energy?
Answer
Yes. Consider a system with two particles. In one microstate, particle A has an energy of 1 unit, and Particle B has an energy of 2 units. In another microstate, particle A has an energy of 2 units, while Particle B has an energy of 1 unit. These two distinct microstates (or configurations) clearly have the same total energy of 3 units. Microstates that share the same energy are called degenerate states.
Since different microstates can be degenerate, the probability that a system has energy is:
where is the degeneracy of
.