Term symbols are notations representing energy levels of a particular electron configuration of an atom.
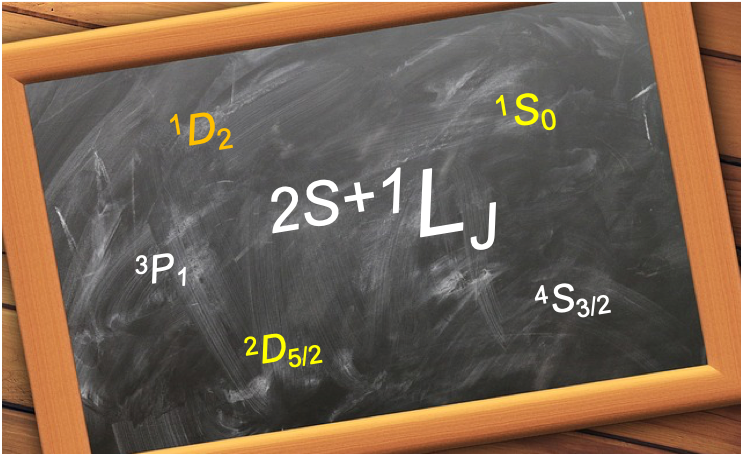
Based on Russell Saunders coupling, a term symbol can be expressed either as:
or
where is called the multiplicity of the term symbol,
is the total spin angular momentum quantum number,
is the total orbital angular momentum quantum number and
is the total angular momentum quantum number.
Each value of is further assigned a letter:
| L | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Letter | S | P | D | F | G | H | I | K | L |
Energy levels denoted by eq291 ignore spin-orbit coupling and are called terms, while those denoted by eq292 take into account spin-orbit coupling and are known as levels. Eq291 implies that for a particular electron configuration of an atom, states with the same set of angular momentum quantum numbers and
have the same energy. We have shown in an earlier article how this is possible. When spin-orbit coupling effects are considered, degenerate states corresponding to a term are split into multiple levels. From eq248 and eq289, energy levels of a particular electron configuration of an atom are dependent on the quantum numbers
,
and
.

Question
Write the term symbols for i) the ground state of the hydrogen atom, and ii) the excited state of the hydrogen atom with the electron in the 2p orbital.
Answer
For the ground state of hydrogen, where and
, it is denoted by
. For the excited state, the electron can be in any of the three degenerate 2p orbitals with either an up spin or a down spin. We would therefore expect two term symbols. The first symbol is
, while the second symbol is obtained using the Clebsch-Gordan series of eq219 and is
.

Question
Why is a term symbol not described by the principal quantum number ?
Answer
Term symbols focus on the variation of energy resulting from the arrangement and interaction of electrons in subshells. These arrangements, known as microstates, depend on whether the electrons are equivalent (belonging to the same subshell) or non-equivalent (belonging to different subshells). For example, the electrons in the configuration are equivalent, while those in
are not. The term symbols for
and
are
and
respectively. Although the term symbols for
and
are the same, the energies of the terms for
, which are determined spectroscopically, differ from those for
. Therefore, while the energy associated with
does influence the overall energy of the electron within the atom, it doesn’t directly contribute to the variation in energies of electrons within the subshells.
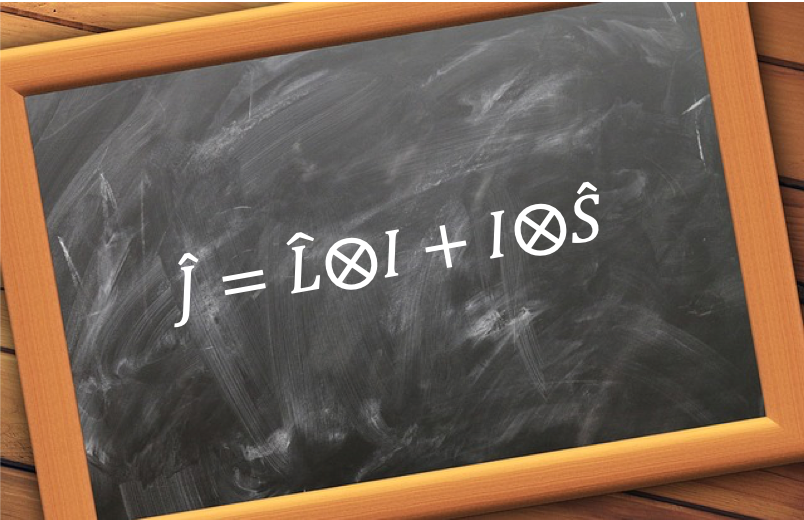

 We shall now show that
We shall now show that